题目内容
若二次函数y=-（x-a）2+a-1的顶点在第四象限，则a的取值范围为（ ）
| A、a＞1 | B、a＜0 |
| C、0＜a＜1 | D、无法确定 |
考点：二次函数的性质
专题：
分析：根据第四象限内点的坐标特征列出关于k的不等式组，解此不等式组即可得到a的取值范围．
解答：解：将二次函数的表达式配方，得y=-（x-a）2+a-1，
∴二次函数图象的顶点坐标是（a，a-1）．
∴
解得 0＜a＜1．
故选C．
∴二次函数图象的顶点坐标是（a，a-1）．
∴
|
解得 0＜a＜1．
故选C．
点评：本题主要考查了二次函数的性质，第四象限内点的坐标特征及一元一次不等式组的解法，正确求出二次函数y=-（x-a）2+a-1的顶点坐标是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
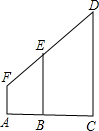如图，EB=5，AB=4，AC=12，AF=1.6，求CD的长．
如图，BC⊥ED于O，∠A=27°，∠D=20°，则∠B=
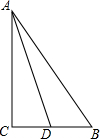如图，在△ABC中，∠C=90°，AD平分∠BAC交BC于D，若BC=64，且BD：CD=9：7，则点D到AB边的距离为
如图，在一块正方形ABCD木板上要贴三种不同的墙纸，正方形EFCG部分贴A型墙纸，△ABE部分贴B型墙纸，其余部分贴C型墙纸．A型、B型、C型三种墙纸的单价分别为每平方60元、80元、40元．
已知A是双曲线
观察月历：