题目内容
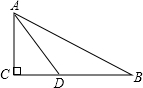如图，在Rt△ABC中，∠BCA=90°，点D是BC上一点，AD=BD，若AB=8，BD=5，则CD=考点：勾股定理
专题：
分析：设CD=x，在Rt△ACD和Rt△ABC中，利用勾股定理列式表示出AC2，然后解方程即可．
解答：解：设CD=x，则BC=5+x，
在Rt△ACD中，AC2=AD2-CD2=25-x2，
在Rt△ABC中，AC2=AB2-BC2=64-（5+x）2，
所以，25-x2=64-（5+x）2，
解得x=1.4，
即CD=1.4．
故答案为：1.4．
在Rt△ACD中，AC2=AD2-CD2=25-x2，
在Rt△ABC中，AC2=AB2-BC2=64-（5+x）2，
所以，25-x2=64-（5+x）2，
解得x=1.4，
即CD=1.4．
故答案为：1.4．
点评：本题考查了勾股定理，熟记定理并在两个三角形列出等式表示出AC2，然后列出方程是解题的关键．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
已知a、b、c在数轴上的位置如图所示，试求|a|+|c-3|+|b|的值．
如图，BC⊥ED于O，∠A=27°，∠D=20°，则∠B=解方程6（1-
）=1，去括号得（ ）
| 1-x |
| 3 |
| A、6-2+2x=6 | ||
| B、6-2+2x=1 | ||
C、6-
| ||
| D、6-2-x=1 |
如图，在一块正方形ABCD木板上要贴三种不同的墙纸，正方形EFCG部分贴A型墙纸，△ABE部分贴B型墙纸，其余部分贴C型墙纸．A型、B型、C型三种墙纸的单价分别为每平方60元、80元、40元．