题目内容
已知点P(m,n)是反比例函数y=
(x>0)图象上的动点,PA∥x轴,PB∥y轴,分别交反比例函数y=
(x>0)的图象于点A、B,点C是直线y=2x上的一动点.
(1)请用含m的代数式分别表示P、A、B三点的坐标;
(2)在点P运动过程中,连接AB,△PAB的面积是否变化?若不变,请求出△PAB的面积;若改变,请说明理由;
(3)在点P运动过程中,以点P、A、C、B为顶点的四边形能否为平行四边形?若能,请求出此时的m值;若不能,请说明理由.

| 6 |
| x |
| 3 |
| x |
(1)请用含m的代数式分别表示P、A、B三点的坐标;
(2)在点P运动过程中,连接AB,△PAB的面积是否变化?若不变,请求出△PAB的面积;若改变,请说明理由;
(3)在点P运动过程中,以点P、A、C、B为顶点的四边形能否为平行四边形?若能,请求出此时的m值;若不能,请说明理由.

考点:反比例函数综合题
专题:
分析:(1)将点P(m,n)代入反比例函数y=
(x>0),用m表示出n即可表示出点P的坐标,然后根据PA∥x轴,得到A点的纵坐标为
,然后将点A的纵坐标带人反比例函数的解析式y=
(x>0)即可得到点A的坐标,同理得到点B的坐标;
(2)根据PA=m-
,PB=
-
=
,利用S△PAB=
PA•PB即可得到答案;
(3)根据四边形PBAC为平行四边形,则有AC∥y轴,从而得到C点横坐标为
,代入y=2x可得C(m,m),然后表示出AC=m-
,PB=
,根据AC=PB列出方程求得m的值即可.
| 6 |
| x |
| 6 |
| m |
| 3 |
| x |
(2)根据PA=m-
| m |
| 2 |
| 6 |
| m |
| 3 |
| m |
| 3 |
| m |
| 1 |
| 2 |
(3)根据四边形PBAC为平行四边形,则有AC∥y轴,从而得到C点横坐标为
| m |
| 2 |
| 6 |
| m |
| 3 |
| m |
解答:解:(1)∵点P(m,n)是反比例函数y=
(x>0)图象上的动点,
∴n=
,
∴点P(m,
);
∵PA∥x轴,
∴A点的纵坐标为
,
将点A的纵坐标带人反比例函数的解析式y=
(x>0)得:
x=
,
∴A(
,
),同理可得:B(m,
);
(2)∵PA=m-
,PB=
-
=
,
∴S△PAB=
PA•PB=
×
×
=
;
(3)∵若四边形PBAC为平行四边形,则有AC∥y轴,
∴C点横坐标为
,
代入y=2x得C(m,m),
此时AC=m-
,PB=
,
由AC=PB,得:m-
=
,
解得:m=3或m=-3(舍去),
∴m=3时,四边形PBAC为平行四边形.
| 6 |
| x |
∴n=
| 6 |
| m |
∴点P(m,
| 6 |
| m |
∵PA∥x轴,
∴A点的纵坐标为
| 6 |
| m |
将点A的纵坐标带人反比例函数的解析式y=
| 3 |
| x |
x=
| m |
| 2 |
∴A(
| m |
| 2 |
| 6 |
| m |
| 3 |
| m |
(2)∵PA=m-
| m |
| 2 |
| 6 |
| m |
| 3 |
| m |
| 3 |
| m |
∴S△PAB=
| 1 |
| 2 |
| 1 |
| 2 |
| m |
| 2 |
| 3 |
| m |
| 3 |
| 4 |
(3)∵若四边形PBAC为平行四边形,则有AC∥y轴,
∴C点横坐标为
| m |
| 2 |
代入y=2x得C(m,m),
此时AC=m-
| 6 |
| m |
| 3 |
| m |
由AC=PB,得:m-
| 6 |
| m |
| 3 |
| m |
解得:m=3或m=-3(舍去),
∴m=3时,四边形PBAC为平行四边形.
点评:本题考查了反比例函数的综合知识,题目中根据平行坐标轴的直线上的点的坐标特点表示出有关点的坐标是解答本题的关键,难度中等偏上.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
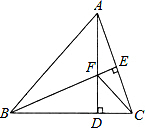 如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.
如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.

 如图,在△ABC中,PD⊥AC,PE⊥AB,PF⊥BC,PD=PE=PF,求证:∠BPC=90°+
如图,在△ABC中,PD⊥AC,PE⊥AB,PF⊥BC,PD=PE=PF,求证:∠BPC=90°+