Question

18．如图1，AB为半圆O的直径，D为BA的延长线上一点，DC为半圆O的切线，切点为C．
（1）求证：∠ACD=∠B；
（2）如图2，∠BDC的平分线分别交AC，BC于点E，F，求∠CEF的度数．

Answer 1

分析 （1）连接OC，利用等角的余角相等即可证明；
（2）根据三角形的外角的性质证明∠CEF=∠CFE即可求解．

解答 （1）证明：如图1中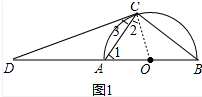，连接OC．
∵OA=OC，
∴∠1=∠2，
∵CD是⊙O切线，
∴OC⊥CD，
∴∠DCO=90°，
∴∠3+∠2=90°，
∵AB是直径，
∴∠1+∠B=90°，
∴∠3=∠B．
（2）解：①∵∠CEF=∠ECD+∠CDE，∠CFE=∠B+∠FDB，
∵∠CDE=∠FDB，∠ECD=∠B，
∴∠CEF=∠CFE，
∵∠ECF=90°，
∴∠CEF=∠CFE=45°．

点评 本题考查切线的性质以及三角形的外角的性质，三角形的外角等于不相邻的两个内角的和．