题目内容
如图，已知∠1=20°，∠2=27°，∠A=52°，则∠BDC的度数是考点：三角形内角和定理,三角形的外角性质
专题：计算题
分析：连结AD，如图，根据三角形外角性质得∠5=∠1+∠3，∠6=∠2+∠4，则∠5+∠6=∠1+∠3+∠4+∠2=∠1+∠A+∠2，然后把∠1=20°，∠2=27°，∠A=52°代入计算即可．
解答：
解：连结AD，如图，
∵∠5=∠1+∠3，∠6=∠2+∠4，
∴∠5+∠6=∠1+∠3+∠4+∠2
=∠1+∠A+∠2
=20°+27°+52°
=99°．
故答案为99°．
解：连结AD，如图，∵∠5=∠1+∠3，∠6=∠2+∠4，
∴∠5+∠6=∠1+∠3+∠4+∠2
=∠1+∠A+∠2
=20°+27°+52°
=99°．
故答案为99°．
点评：本题考查了三角形内角和定理：三角形内角和是180°．灵活应用三角形外角性质．
练习册系列答案
相关题目
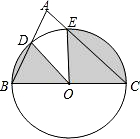如图，以BC为直径的⊙O与△ABC的另两边分别相交于点D、E．若∠A=72°，BC=4．求图中阴影部分的总周长和总面积（结果保留π）
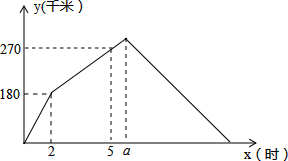甲、乙两车都从同一地点沿同一路线驶向同一目的地，甲车先行，一段时间后，乙车开始行驶，甲车到达目的地后，乙车走完了全程的
如图，点E，F分别是矩形ABCD的边AD，BC的三等分点（距D、C近），若矩形ABFE与矩形ABCD相似，则矩形ABCD的AD：AB是
如图，E是平行四边形ABCD的AB边的中点，且AD=10cm，那么OE=