题目内容
16. 如图,△ABC中,∠ABC和∠ACB的角平分线相交于点O,DE经过O点,且DE∥BC.
如图,△ABC中,∠ABC和∠ACB的角平分线相交于点O,DE经过O点,且DE∥BC.(1)请指出图中的两个等腰三角形.
(2)请选择(1)中的一个三角形,说明它是等腰三角形的理由.
(3)如果△ABC的周长是26,△ADE的周长是18,请求出BC的长.
分析 (1)△BOD和△COE是等腰三角形
(2)根据角平分线和平行线的性质来证明;
(3)由(2)的结论代入到△ABC的周长中,列方程,可以得出BC的长.
解答 解:(1)△BOD和△COE;
(2)∵BO是∠ABC的平分线,
∴∠DBO=∠OBC,
又∵DE‖BC,
∴∠DOB=∠OBC,
∴∠DBO=∠DOB,
∴BD=OD,
∴△BOD 是等腰三角形;
同理可得:△COE是等腰三角形;
(3)∵△BOD和△COE是等腰三角形,
∴BD=OD,CE=OE,
∴BD+CE=OD+OE,
即 BD+CE=DE,
∵△ABC的周长=AD+BD+BC+AE+CE,
=AD+BC+AE+DE,
=△ADE的周长+BC,
∵△ABC的周长是26,△ADE的周长是18,
即 26=18+BC,
∴BC=8.
点评 本题考查了角平分线的定义、平行线的性质、等腰三角形的性质和判定,属于基础题,难度不大;根据角平分线的定义可得分成的两个角相等与平行线的内错角相等相结合,得到等腰三角形,从而得出结论.

练习册系列答案
相关题目
6.碧华学校在校师生约为0.3万人,近似数0.3万是精确到( )
| A. | 十分位 | B. | 百分位 | C. | 千位 | D. | 百位 |
1.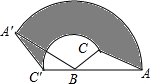 如图,在△ABC中,AB=12cm,BC=6cm,∠ABC=30°,把△ABC以点B为中心按逆时针方向旋转,使点C旋转到AB边的延长线上的C′处,那么AC边扫过的图形(图中阴影部分)的面积是( )cm2.(结果保留π)
如图,在△ABC中,AB=12cm,BC=6cm,∠ABC=30°,把△ABC以点B为中心按逆时针方向旋转,使点C旋转到AB边的延长线上的C′处,那么AC边扫过的图形(图中阴影部分)的面积是( )cm2.(结果保留π)
 如图,在△ABC中,AB=12cm,BC=6cm,∠ABC=30°,把△ABC以点B为中心按逆时针方向旋转,使点C旋转到AB边的延长线上的C′处,那么AC边扫过的图形(图中阴影部分)的面积是( )cm2.(结果保留π)
如图,在△ABC中,AB=12cm,BC=6cm,∠ABC=30°,把△ABC以点B为中心按逆时针方向旋转,使点C旋转到AB边的延长线上的C′处,那么AC边扫过的图形(图中阴影部分)的面积是( )cm2.(结果保留π)| A. | 15π | B. | 60π | C. | 45π | D. | 75π |
8.下列式子中去括号错误的是( )
| A. | 5x-(x-2y)=5x-x+2y | B. | 2a2+(3a-b)=2a2+3a-b | ||
| C. | (x-2y)-(x2-y2)=x-2y-x2+y2 | D. | 3x2-3(x+6)=3x2-3x-6 |
 如图,已知二次函数y=x2-4x-5与x轴交于A,B两点,则AB的长度为6.
如图,已知二次函数y=x2-4x-5与x轴交于A,B两点,则AB的长度为6. 有理数a、b在数轴上的对应点位置如图所示
有理数a、b在数轴上的对应点位置如图所示 已知抛物线y=x2+bx+c的部分图象如图所示,若-3<y<0,则x的取值范围是-1<x<0或2<x<3.
已知抛物线y=x2+bx+c的部分图象如图所示,若-3<y<0,则x的取值范围是-1<x<0或2<x<3.