题目内容
18. 如图,正方形ABCD中,AB=2,M是AB的中点.连MC,点P,Q分别是MC,BC上任意一点,则PQ+PB的最小值为$\frac{8}{5}$.
如图,正方形ABCD中,AB=2,M是AB的中点.连MC,点P,Q分别是MC,BC上任意一点,则PQ+PB的最小值为$\frac{8}{5}$.
分析 如图,作点B关于CM的对称点B′,作B′Q⊥BC与CM的交点即为所求的点P,根据相似三角形的性质得到$\frac{BB′}{CM}=\frac{B′Q}{BC}$,由M是AB的中点,得到BM=1,根据勾股定理得到CM=$\sqrt{B{M}^{2}+B{C}^{2}}$=$\sqrt{5}$,由三角形的面积公式得到BB′=2×$\frac{BM•BC}{CM}$=$\frac{4\sqrt{5}}{5}$,于是得到结论.
解答 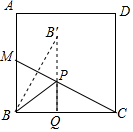 解:如图,作点B关于CM的对称点B′,作B′Q⊥BC与CM的交点即为所求的点P,
解:如图,作点B关于CM的对称点B′,作B′Q⊥BC与CM的交点即为所求的点P,
∵∠B′+∠B′BQ=90°,
∠BCM+∠B′BQ=90°,
∴∠B′=∠BCM,
又∵∠ABC=∠BQB′=90°,
∴△BCM∽△B′QB,
∴$\frac{BB′}{CM}=\frac{B′Q}{BC}$,
∵M是AB的中点,
∴BM=1,
∴CM=$\sqrt{B{M}^{2}+B{C}^{2}}$=$\sqrt{5}$,
∴BB′=2×$\frac{BM•BC}{CM}$=$\frac{4\sqrt{5}}{5}$,
∴$\frac{\frac{4\sqrt{5}}{5}}{\sqrt{5}}$=$\frac{B′Q}{2}$,
∴B′Q=$\frac{8}{5}$,
∴PQ+PB的最小值=$\frac{8}{5}$,
故答案为:$\frac{8}{5}$.
点评 本题考查了轴对称-最短路线问题,正方形的性质,相似三角形的判定与性质,三角形的面积公式,确定出点P的位置是解题的关键.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
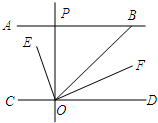 如图,AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=40°,则下列结论:
如图,AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=40°,则下列结论: 一副三角板按如图方式摆放,得到△ABD和△BCD,其中∠ADB=∠BCD=90°,∠A=60°,∠CBD=45°,E为AB的中点,过点E作EF⊥CD于点F.若AD=4cm,则EF的长为($\sqrt{2}$+$\sqrt{6}$)cm.
一副三角板按如图方式摆放,得到△ABD和△BCD,其中∠ADB=∠BCD=90°,∠A=60°,∠CBD=45°,E为AB的中点,过点E作EF⊥CD于点F.若AD=4cm,则EF的长为($\sqrt{2}$+$\sqrt{6}$)cm.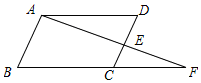 如图,点C、E分别是线段BF、线段CD的中点,AD∥BF.
如图,点C、E分别是线段BF、线段CD的中点,AD∥BF.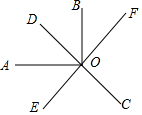 如图,已知直线CD、EF相交于点O,OA⊥OB,且OE平分∠AOC,若∠EOC=60°,则∠BOF=30°.
如图,已知直线CD、EF相交于点O,OA⊥OB,且OE平分∠AOC,若∠EOC=60°,则∠BOF=30°.