题目内容
15.某商店经营T恤衫,己知成批购进时单价是20元,根据市场调查,销售量与销售单价满足如下关系:在一段时间内,单价是35元时,销售量是600件.而单价每降低1元,就可以多销售200件.若设销售单价为x(20≤x≤35的整数)元,该商店所获利润为y元.(1)求y与x的函数关系式;
(2)当销售价为多少时,利润最大?并求出最大利润.
分析 (1)根据“利润=单件利润×销售数量”即可列出y关于x的函数关系式;
(2)利用配方法将(1)中的函数关系式变形为y=-200(x-29)2+16200,再根据二次函数的性质即可解决最值问题.
解答 解:(1)根据已知得:y=(x-20)[600+200×(35-x)]=-200x2+11600x-152000(20≤x≤35且x为整数).
(2)由(1)可得:y=-200x2+11600x-152000=-200(x-29)2+16200,
∵a=-200<0,
∴当x=29时,y取最大值16200.
答:当销售价为29元时,利润最大,最大利润为16200元.
点评 本题考查了二次函数的应用以及二次函数的性质,根据数量关系列出y关于x的二次函数关系式是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
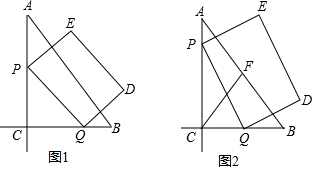
 (1)图中有哪几对互余的角?
(1)图中有哪几对互余的角?