题目内容
18. 已知:如图,点D、E分别在AB、AC上,BE与CD相交于点O,∠1=∠2,∠B=∠C.求证:OD=OE.
已知:如图,点D、E分别在AB、AC上,BE与CD相交于点O,∠1=∠2,∠B=∠C.求证:OD=OE.
分析 先根据AAS证明△AOC≌△AOB,得到OC=OB,再证明△COE≌△BOD即可.
解答 证明:∵∠1=∠2,∠COE=∠BOD,
∴∠AOC=∠AOB,
在△AOC和△AOB中,
$\left\{\begin{array}{l}{∠AOC=∠AOB}\\{∠B=∠C}\\{AO=AO}\end{array}\right.$,
∴△AOC≌△AOB(AAS),
∴OC=OB,
在△COE和△BOD中,
$\left\{\begin{array}{l}{∠COE=∠BOD}\\{OC=OB}\\{∠B=∠C}\end{array}\right.$,
∴△COE≌△BOD(ASA),
∴OD=OE.
点评 本题考查了全等三角形的判定,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
8.在下面图形:线段、等腰三角形、正方形、平行四边形、梯形中是中心对称图形的有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
6.在同一直角坐标系中,P、Q分别是y=-x+3与y=3x-5的图象上的点,且P、Q关于x轴对称,则点P的坐标是( )
| A. | (-$\frac{1}{2}$,$\frac{7}{2}$) | B. | (-2,5) | C. | (1,2) | D. | (-4,7) |
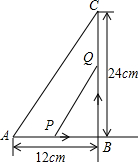 如图,在△ABC中,∠B=90°,点P从点A开始沿AB边向点B以2cm/s的速度移动,Q从点B开始沿BC向C点以4cm/s的速度移动,如果点P、Q分别从A、B同时出发,几秒钟后,△PBQ的面积等于16cm2?
如图,在△ABC中,∠B=90°,点P从点A开始沿AB边向点B以2cm/s的速度移动,Q从点B开始沿BC向C点以4cm/s的速度移动,如果点P、Q分别从A、B同时出发,几秒钟后,△PBQ的面积等于16cm2?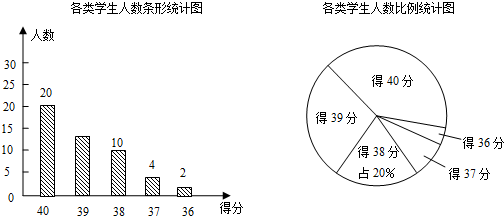
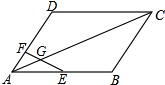 如图,在?ABCD中,E为AB的中点,点F在AD上,EF交AC于点G,AF=2,DF=4,AG=3,求AC的长.
如图,在?ABCD中,E为AB的中点,点F在AD上,EF交AC于点G,AF=2,DF=4,AG=3,求AC的长.