题目内容
把下列二次函数化成顶点式，即y=a（x+m）2+k的形式，并写出他们顶点坐标及最大值或最小值．
（1）y=-2x-3+
x2
（2）y=-2x2-5x+7
（3）y=ax2+bx+c（a≠0）
（1）y=-2x-3+
| 1 |
| 2 |
（2）y=-2x2-5x+7
（3）y=ax2+bx+c（a≠0）
考点：二次函数的三种形式
专题：
分析：利用配方法先提出二次项系数，再加上一次项系数的一半的平方来凑完全平方式，可把一般式转化为顶点式，从而求出函数图象的顶点坐标及最值．
解答：解：（1）y=-2x-3+
x2
=
（x2-4x+4）-2-3
=
（x-2）2-5，
顶点坐标是（2，-5），最小值是-5；
（2）y=-2x2-5x+7
=-2（x2+
x+
）+
+7
=-2（x+
）2+
，
顶点坐标是（-
，
），最大值是
；
（3）y=ax2+bx+c
=a（x2+
x+
）-
+c
=a（x+
）2+
，
顶点坐标是（-
，
），
当a＜0时，最大值是
；当a＞0时，最小值是
．
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
顶点坐标是（2，-5），最小值是-5；
（2）y=-2x2-5x+7
=-2（x2+
| 5 |
| 2 |
| 25 |
| 16 |
| 25 |
| 8 |
=-2（x+
| 5 |
| 4 |
| 81 |
| 8 |
顶点坐标是（-
| 5 |
| 4 |
| 81 |
| 8 |
| 81 |
| 8 |
（3）y=ax2+bx+c
=a（x2+
| b |
| a |
| b2 |
| 4a2 |
| b2 |
| 4a |
=a（x+
| b |
| 2a |
| 4ac-b2 |
| 4a |
顶点坐标是（-
| b |
| 2a |
| 4ac-b2 |
| 4a |
当a＜0时，最大值是
| 4ac-b2 |
| 4a |
| 4ac-b2 |
| 4a |
点评：此题主要考查了二次函数的性质，解题的关键是利用配方法将一般式化为顶点式．
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
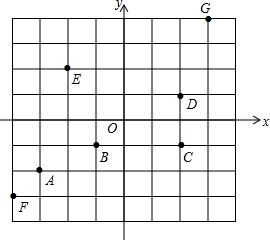看图完成任务：
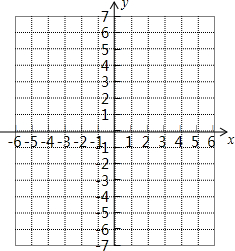在给定的直角坐标系中描出下列各点，并将各组内的点用线段依次连接起来．
如图，点P为△ABC内一点，且PB=AB．求证：AC＞PC．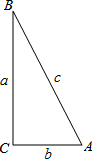
在如图的直角三角形中，我们知道sinα=