题目内容
在平面直角坐标系中,⊙O的圆心在原点上,半径为2,则下面各点在⊙O上的是( )
| A、(1,1) | ||||
| B、(-1,3) | ||||
| C、(-2,-1) | ||||
D、(
|
考点:点与圆的位置关系,坐标与图形性质
专题:
分析:根据点的坐标性质结合勾股定理得出斜边长,进而得出点与⊙O关系.
解答: 解:如图所示:A、(1,1)点构成直角三角形的斜边为
解:如图所示:A、(1,1)点构成直角三角形的斜边为
,小于2,故不在⊙O上,故此选项错误;
B、(-1,3)点构成直角三角形的斜边为
,大于2,故不在⊙O上,故此选项错误;
C、(-2,-1)点构成直角三角形的斜边为
,大于2,故不在⊙O上,故此选项错误;
D、(
,-
)点构成直角三角形的斜边为2,等于2,故在⊙O上,故此选项正确;
故选:D.
 解:如图所示:A、(1,1)点构成直角三角形的斜边为
解:如图所示:A、(1,1)点构成直角三角形的斜边为| 2 |
B、(-1,3)点构成直角三角形的斜边为
| 10 |
C、(-2,-1)点构成直角三角形的斜边为
| 5 |
D、(
| 2 |
| 2 |
故选:D.
点评:此题主要考查了点与圆的位置关系,点与圆的位置关系有3种.设⊙O的半径为r,点P到圆心的距离OP=d,则有:
①点P在圆外?d>r,②点P在圆上?d=r,③点P在圆内?d<r.
①点P在圆外?d>r,②点P在圆上?d=r,③点P在圆内?d<r.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列图形中,是轴对称图形,又是中心对称图形的是( )
A、 |
B、 |
C、 |
D、 |
如图,把图①中的△ABC经过一定的变换得到图②中的△A′B′C′,如果图①中△ABC上点P的坐标为(a,b),那么这个点在图②中的对应点P′的坐标为( )
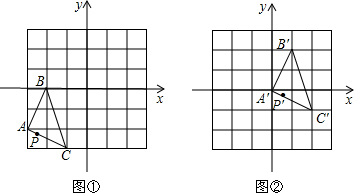

| A、(a+2,b+3) |
| B、(a-3,b-2) |
| C、(a+3,b+2) |
| D、(a-2,b-3) |
下列四种标志图案中,既是轴对称图形又是中心对称图形的是( )
A、 中国移动 |
B、 中国联通 |
C、 中国网通 |
D、 中国电信 |
 如图,在矩形ABCD中,已知AB=12,AD=8,如果将矩形沿直线l翻折后,点A落在边CD的中点E处,直线l与分别边AB、AD交于点M、N,那么MN的长为
如图,在矩形ABCD中,已知AB=12,AD=8,如果将矩形沿直线l翻折后,点A落在边CD的中点E处,直线l与分别边AB、AD交于点M、N,那么MN的长为