Question

15．如图，△ABC中，AB=BC=5，AC=6，过点A作AD∥BC，点P、Q分别是射线AD、线段BA上的动点，且AP=BQ，过点P作PE∥AC交线段AQ于点O，连接PQ，设△POQ面积为y，AP=x．
（1）用含x的代数式表示PO；
（2）连接NE，若△PQE与△POQ相似，求AP的长．

Answer 1

分析 （1）首先根据AD∥BC，PE∥AC，判定四边形APEC是平行四边形，从而得到AC=PE=6，AP=EC=x，然后根据平行线分线段成比例定理列出比例式用含x的代数式表示PO；
（2）根据当0＜x＜$\frac{5}{2}$时，由AP=BQ=x，AQ=BE=5-x，∠PAQ=∠QBE可得△PAQ≌△QBE，于是PQ=QE，可得若△PQE与△POQ相似，只有△PQE∽△POQ，于是得$\frac{6}{5}$x=5-2x，解得x的值即可．

解答 解：（1）∵AD∥BC，PE∥AC，
∴四边形APEC是平行四边形，
∴AC=PE=6，AP=EC=x，
∵$\frac{PA}{BE}$=$\frac{PO}{OE}$，
∴$\frac{x}{5-x}$=$\frac{PO}{6-PO}$，
解得：PO=$\frac{6}{5}$x；
（2）当0＜x＜$\frac{5}{2}$时，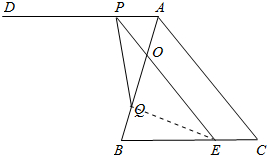
由AP=BQ=x，AQ=BE=5-x，∠PAQ=∠QBE，
可得△PAQ≌△QBE，于是PQ=QE，
由于∠QPO=∠EPQ，
所以若△PQE与△POQ相似，只有△PQE∽△POQ，
可得OP=OQ，
于是得，$\frac{6}{5}$x=5-2x，
解得：x=$\frac{25}{16}$；
同理当$\frac{5}{2}$＜x＜5时，可得x=$\frac{25}{4}$（不合题意，舍去）．
所以，若△PQE与△POQ相似，AP的长为$\frac{25}{16}$．

点评 本题主要考查了相似三角形的综合知识，根据实际问题列一次函数关系式等，本题关键在于作出辅助线，找出等量关系．