题目内容
15.下列等式中,从左到右的变形是分解因式的是( )| A. | (x+1)(x-2)=x2-x-2 | B. | 4a2b3=4a2•b3 | C. | x2-2x+1=(x-1)2 | D. | x2-3x+2=x(x-3)+2 |
分析 依据因式分解的定义:将一个多项式分解成几个整式乘积的形式称为分解因式.对A、B、C、D四个选项进行求解.
解答 解:A、(x+1)(x-2)=x2-x-2是整式相乘,故A错误;
B、4a2b3=4a2•b3,不是因式分解,故B错误;
C、x2-2x+1=(x-1)2,故C正确;
D、x2-3x+2=x(x-3)+2,等式右边有加号,故D错误;
故选:C.
点评 此题主要考查因式分解的意义,要注意因式分解的一般步骤:
①如果一个多项式各项有公因式,一般应先提取公因式;
②如果一个多项式各项没有公因式,一般应思考运用公式、十字相乘法;如果多项式有两项应思考用平方差公式,如果多项式有三项应思考用公式法或用十字相乘法; 如果多项式超过三项应思考用完全平方公式法;
③分解因式时必须要分解到不能再分解为止.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.$\sqrt{4-x}$在实数范围内有意义,则x的取值范围是( )
| A. | x≥4 | B. | x>4 | C. | x≤4 | D. | x<4 |
3.当x=( )时,分式$\frac{x+3}{|x|-2}$无意义( )
| A. | x=-3 | B. | x=2 | C. | x=-2 | D. | x=±2 |
4.如果一个36°角的两条边与∠B的两条边分别平行,则∠B为( )
| A. | 36° | B. | 144° | C. | 36°或144° | D. | 36°或54° |
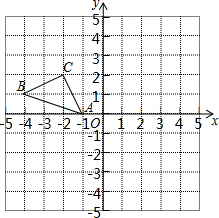 正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:
正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题: