题目内容
2.先化简,再求值:($\frac{x+2}{{x}^{2}-2x}$-$\frac{x-1}{{x}^{2}-4x+4}$)÷$\frac{{x}^{2}-16}{{x}^{2}+4x}$,其中x是不等式组$\left\{{\begin{array}{l}{2x-1≥3}\\{2-3x≥-10}\end{array}}$的整数解.分析 原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,求出不等式组的整数解确定出x的值,代入计算即可求出值.
解答 解:原式=$\frac{(x+2)(x-2)-x(x-1)}{x(x-2)^{2}}$•$\frac{x(x+4)}{(x+4)(x-4)}$=$\frac{x-4}{x(x-2)^{2}}$•$\frac{x(x+4)}{(x+4)(x-4)}$=$\frac{1}{(x-2)^{2}}$,
由不等式组$\left\{{\begin{array}{l}{2x-1≥3}\\{2-3x≥-10}\end{array}}$,解得:2≤x≤4,即整数解为2,3,4,
当x=3时,原式=1.
点评 此题考查了分式的化简求值,以及一元一次不等式组的整数解,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
13.已知a>b,则下列结论中错误的是( )
| A. | a-5>b-5 | B. | 2a>2b | C. | a-b>0 | D. | ac>bc |
17.把分式$\frac{2a}{a+b}$中的a、b都扩大4倍,则分式的值( )
| A. | 扩大8倍 | B. | 不变 | C. | 缩小4倍 | D. | 扩大4倍 |
14.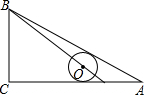 在△ABC中,∠C=90°,∠A=30°,BC=1,点P在AC上,∠PBC=45°,⊙O的圆心在线段BP上,且⊙O与AB,AC都相切,则⊙O的半径是( )
在△ABC中,∠C=90°,∠A=30°,BC=1,点P在AC上,∠PBC=45°,⊙O的圆心在线段BP上,且⊙O与AB,AC都相切,则⊙O的半径是( )
 在△ABC中,∠C=90°,∠A=30°,BC=1,点P在AC上,∠PBC=45°,⊙O的圆心在线段BP上,且⊙O与AB,AC都相切,则⊙O的半径是( )
在△ABC中,∠C=90°,∠A=30°,BC=1,点P在AC上,∠PBC=45°,⊙O的圆心在线段BP上,且⊙O与AB,AC都相切,则⊙O的半径是( )| A. | 2-$\sqrt{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{\sqrt{3}}{6}$ |
11.下列调查中,适宜采用全面调查方式的是( )
| A. | 了解北京市中学生的视力情况 | |
| B. | 调查某品牌食品的色素含量是否符合国家标准 | |
| C. | 了解全班同学参加社会实践活动时间 | |
| D. | 调查春节联欢晚会的收视率 |
 在△ABC中,∠A=$\frac{1}{2}$∠B=∠ACB+20°,CD为∠ACB的平分线,求∠A及∠BDC的度数.
在△ABC中,∠A=$\frac{1}{2}$∠B=∠ACB+20°,CD为∠ACB的平分线,求∠A及∠BDC的度数.