题目内容
6.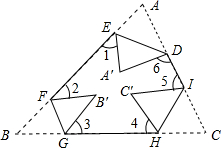 如图所示,把一个三角形纸片ABC的三个顶角向内折叠之后(3个顶点不重合),那么图中∠1+∠2+∠3+∠4+∠5+∠6的度数和是( )
如图所示,把一个三角形纸片ABC的三个顶角向内折叠之后(3个顶点不重合),那么图中∠1+∠2+∠3+∠4+∠5+∠6的度数和是( )| A. | 180° | B. | 270° | C. | 360° | D. | 540° |
分析 由折叠可知∠1+∠2+∠3+∠4+∠5+∠6等于六边形的内角和减去(∠B'FG+∠B'GF)以及(∠C'HI+∠C'IH)和(∠A'DE+∠A'ED),再利用三角形的内角和定理即可求解.
解答 解:由题意知,
∠1+∠2+∠3+∠4+∠5+∠6=720°-(∠B'FG+∠B'GF)-(∠C'HI+∠C'IH)-(∠A'DE+∠A'ED)=720°-(180°-∠B')-(180°-C')=(180°-A')=180°+(∠B'+∠C'+∠A')
又∵∵∠B=∠B',∠C=∠C',∠A=∠A',
∠A+∠B+∠C=180°,
∴∠1+∠2+∠3+∠4+∠5+∠6=360°.
故选C.
点评 本题考查的是三角形内角和定理,熟知图形翻折变换的性质是解答此题的关键.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
12.在平面直角坐标系中,点P(x2+1,-2)所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
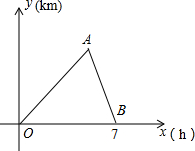 已知一辆汽车从A地匀速行驶到B地后原路返回到A地,点A的横坐标为4,汽车在从A地行驶到B地的途中经过C地,汽车两次经过C地的间隔时间为$\frac{7}{2}$小时,设汽车离开A地的时间为x小时,离A地的距离为y千米,如图所示.
已知一辆汽车从A地匀速行驶到B地后原路返回到A地,点A的横坐标为4,汽车在从A地行驶到B地的途中经过C地,汽车两次经过C地的间隔时间为$\frac{7}{2}$小时,设汽车离开A地的时间为x小时,离A地的距离为y千米,如图所示.