题目内容
11.已知|c+$\sqrt{5}$|+|c-$\sqrt{5}$|=6,求c的值.分析 分类讨论x的范围,利用绝对值的代数意义化简,求出满足题意x的范围即可.
解答 解:∵|c+$\sqrt{5}$|+|c-$\sqrt{5}$|=6,
∴|c+$\sqrt{5}$|≥0,令|c+$\sqrt{5}$|=0,c=-$\sqrt{5}$,
∴|c-$\sqrt{5}$|≥0,令|c-$\sqrt{5}$|=0,c=$\sqrt{5}$,
当c≤-$\sqrt{5}$时,整理得:|c+$\sqrt{5}$|+|c-$\sqrt{5}$|=-c-$\sqrt{5}$-c+$\sqrt{5}$=-2c=6,c=-3;
当-$\sqrt{5}$≤x≤$\sqrt{5}$时,|c+$\sqrt{5}$|+|c-$\sqrt{5}$|=c+$\sqrt{5}$-c+$\sqrt{5}$=2$\sqrt{5}$=6,不合题意舍去;
当c$>\sqrt{5}$时,|c+$\sqrt{5}$|+|c-$\sqrt{5}$|=c+$\sqrt{5}$+c-$\sqrt{5}$=2c=6,c=3;
综上所述,c等于3或-3.
点评 此题考查二次根式的应用,关键是根据二次根式的性质分析.

练习册系列答案
相关题目
6.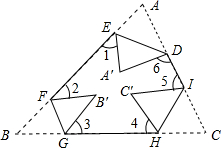 如图所示,把一个三角形纸片ABC的三个顶角向内折叠之后(3个顶点不重合),那么图中∠1+∠2+∠3+∠4+∠5+∠6的度数和是( )
如图所示,把一个三角形纸片ABC的三个顶角向内折叠之后(3个顶点不重合),那么图中∠1+∠2+∠3+∠4+∠5+∠6的度数和是( )
 如图所示,把一个三角形纸片ABC的三个顶角向内折叠之后(3个顶点不重合),那么图中∠1+∠2+∠3+∠4+∠5+∠6的度数和是( )
如图所示,把一个三角形纸片ABC的三个顶角向内折叠之后(3个顶点不重合),那么图中∠1+∠2+∠3+∠4+∠5+∠6的度数和是( )| A. | 180° | B. | 270° | C. | 360° | D. | 540° |
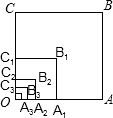 如图,以O为位似中心,将边长为256的正方形OABC依次作位似变换,经第一次变化后得正方形OA1B1C1,其边长OA1缩小为OA的$\frac{1}{2}$,经第二次变化后得正方形OA2B2C2,其边长OA2缩小为OA1的$\frac{1}{2}$,经第三次变化后得正方形OA3B3C3,其边长OA3缩小为OA2的$\frac{1}{2}$,…,依次规律,经第n次变化后,所得正方形OAnBnCn的边长为正方形OABC边长的倒数,则n=16.
如图,以O为位似中心,将边长为256的正方形OABC依次作位似变换,经第一次变化后得正方形OA1B1C1,其边长OA1缩小为OA的$\frac{1}{2}$,经第二次变化后得正方形OA2B2C2,其边长OA2缩小为OA1的$\frac{1}{2}$,经第三次变化后得正方形OA3B3C3,其边长OA3缩小为OA2的$\frac{1}{2}$,…,依次规律,经第n次变化后,所得正方形OAnBnCn的边长为正方形OABC边长的倒数,则n=16.
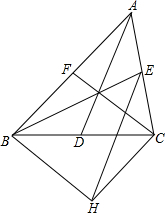 如图,△ABC的三条中线分别为AD、BE、CF,点H为△ABC外一点,且四边形BHCF为平行四边形,连接EH,试探究AD与EH的位置关系.
如图,△ABC的三条中线分别为AD、BE、CF,点H为△ABC外一点,且四边形BHCF为平行四边形,连接EH,试探究AD与EH的位置关系.