题目内容
17.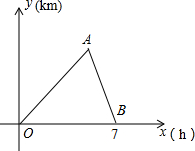 已知一辆汽车从A地匀速行驶到B地后原路返回到A地,点A的横坐标为4,汽车在从A地行驶到B地的途中经过C地,汽车两次经过C地的间隔时间为$\frac{7}{2}$小时,设汽车离开A地的时间为x小时,离A地的距离为y千米,如图所示.
已知一辆汽车从A地匀速行驶到B地后原路返回到A地,点A的横坐标为4,汽车在从A地行驶到B地的途中经过C地,汽车两次经过C地的间隔时间为$\frac{7}{2}$小时,设汽车离开A地的时间为x小时,离A地的距离为y千米,如图所示.(1)汽车在从A地行驶到C地需要2小时.
(2)若从A地与C地的距离为80km,求直线AB的解析式.
分析 (1)设AB之间的距离为a,BC之间的距离为m,根据图象确定从A地到B地的速度为$\frac{a}{4}$,从B地到A地的速度为$\frac{a}{3}$,根据题意得出$\frac{4m}{a}$+$\frac{3m}{a}$=$\frac{7}{2}$,从而求得$\frac{m}{a}$=$\frac{1}{2}$,得出C地在AB的中点处,即可求得从A地行驶到C地需要的时间;
(2)根据待定系数法求得即可.
解答 解(1)设AB之间的距离为a,BC之间的距离为m,
由图象可知从地A到B地用时4小时,从B地到A地用时3小时,
所以从A地到B地的速度为$\frac{a}{4}$,从B地到A地的速度为$\frac{a}{3}$,
所以从C地到B地用时为$\frac{m}{\frac{a}{4}}$=$\frac{4m}{a}$,从B地到C地用时为$\frac{m}{\frac{a}{3}}$=$\frac{3m}{a}$,
根据题意得:$\frac{4m}{a}$+$\frac{3m}{a}$=$\frac{7}{2}$,
解得:$\frac{m}{a}$=$\frac{1}{2}$,
所以C地在AB的中点处,
所以,汽车在从A地行驶到C地需要2小时;
故答案为2;
(2)∵从A地与C地的距离为80km,
∴从A地与C地的距离为160km,
∴A(4,160),
∵B(7,0),
设直线AB的解析式为y=kx+b.
则$\left\{\begin{array}{l}{4k+b=160}\\{7k+b=0}\end{array}\right.$
解得$\left\{\begin{array}{l}{k=-\frac{160}{3}}\\{b=\frac{1120}{3}}\end{array}\right.$,
∴直线AB的解析式为y=-$\frac{160}{3}$x+$\frac{1120}{3}$.
点评 此题考查了一次函数的应用,利用了待定系数法,熟练掌握待定系数法是解本题的关键.

 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 如图,AB=BC=CD=DE=1,且BC⊥AB,CD⊥AC,DE⊥AD,则线段AE的长为( )
如图,AB=BC=CD=DE=1,且BC⊥AB,CD⊥AC,DE⊥AD,则线段AE的长为( )| A. | 1.5 | B. | 2 | C. | 2.5 | D. | 3 |
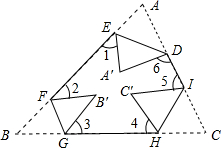 如图所示,把一个三角形纸片ABC的三个顶角向内折叠之后(3个顶点不重合),那么图中∠1+∠2+∠3+∠4+∠5+∠6的度数和是( )
如图所示,把一个三角形纸片ABC的三个顶角向内折叠之后(3个顶点不重合),那么图中∠1+∠2+∠3+∠4+∠5+∠6的度数和是( )| A. | 180° | B. | 270° | C. | 360° | D. | 540° |
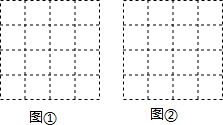 如图,正方形网格中每个小正方形的边长都是1,每个小格的格点叫做“格点”,以格点为顶点分别按下列要求画出三角形.
如图,正方形网格中每个小正方形的边长都是1,每个小格的格点叫做“格点”,以格点为顶点分别按下列要求画出三角形.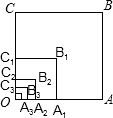 如图,以O为位似中心,将边长为256的正方形OABC依次作位似变换,经第一次变化后得正方形OA1B1C1,其边长OA1缩小为OA的$\frac{1}{2}$,经第二次变化后得正方形OA2B2C2,其边长OA2缩小为OA1的$\frac{1}{2}$,经第三次变化后得正方形OA3B3C3,其边长OA3缩小为OA2的$\frac{1}{2}$,…,依次规律,经第n次变化后,所得正方形OAnBnCn的边长为正方形OABC边长的倒数,则n=16.
如图,以O为位似中心,将边长为256的正方形OABC依次作位似变换,经第一次变化后得正方形OA1B1C1,其边长OA1缩小为OA的$\frac{1}{2}$,经第二次变化后得正方形OA2B2C2,其边长OA2缩小为OA1的$\frac{1}{2}$,经第三次变化后得正方形OA3B3C3,其边长OA3缩小为OA2的$\frac{1}{2}$,…,依次规律,经第n次变化后,所得正方形OAnBnCn的边长为正方形OABC边长的倒数,则n=16. 如图,在△ABC中,以AB为直径的⊙O交AC于点D,过点D作DE⊥BC于点E,且∠BDE=∠A.
如图,在△ABC中,以AB为直径的⊙O交AC于点D,过点D作DE⊥BC于点E,且∠BDE=∠A.