题目内容
18.某网店尝试用单价随天数而变化的销售模式销售一种商品,利用30天的时间销售一种成本为10元/件的商品售后,经过统计得到此商品单价在第x天(x为正整数)销售的相关信息,如表所示:| 销售量n(件) | n=50-x |
| 销售单价m(元/件) | 当1≤x≤20时,m=20+$\frac{1}{2}$x |
| 当21≤x≤30时,m=10+$\frac{420}{x}$ |
(2)求网店销售该商品30天里所获利润y(元)关于x(天)的函数关系式;
(3)这30天中第几天获得的利润最大?最大利润是多少?
分析 (1)分两种情形分别代入解方程即可.
(2)分两种情形写出所获利润y(元)关于x(天)的函数关系式即可.
(3)分两种情形根据函数的性质解决问题即可.
解答 解:(1)分两种情况
①当1≤x≤20时,将m=25代入m=20+$\frac{1}{2}$x,解得x=10
②当21≤x≤30时,25=10+$\frac{420}{x}$,解得x=28
经检验x=28是方程的解
∴x=28
答:第10天或第28天时该商品为25元/件.
(2)分两种情况
①当1≤x≤20时,y=(m-10)n=(20+$\frac{1}{2}$x-10)(50-x)=-$\frac{1}{2}$x2+15x+500,
②当21≤x≤30时,y=(10+$\frac{420}{x}$-10)(50-x)=$\frac{21000}{x}-420$
综上所述:$y=\left\{\begin{array}{l}-\frac{1}{2}{x^2}+15x+500(1≤x≤20)\\ \frac{21000}{x}-420(21≤x≤30)\end{array}\right.$
(3)①当1≤x≤20时
由y=-$\frac{1}{2}$x2+15x+500=-$\frac{1}{2}$(x-15)2+$\frac{1225}{2}$,
∵a=-$\frac{1}{2}$<0,
∴当x=15时,y最大值=$\frac{1225}{2}$,
②当21≤x≤30时
由y=$\frac{21000}{x}$-420,可知y随x的增大而减小
∴当x=21时,y最大值=$\frac{21000}{21}$-420=580元
∵$580<\frac{1225}{2}$
∴第15天时获得利润最大,最大利润为612.5元.
点评 本题考查二次函数的应用、反比例函数的性质等知识,解题的关键是学会构建函数,利用二次函数的性质解决问题,属于中考常考题型.

 如图,将一块直角三角板的直角顶点放在直尺的一边上.如果∠1=50°,那么∠2的度数是( )
如图,将一块直角三角板的直角顶点放在直尺的一边上.如果∠1=50°,那么∠2的度数是( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
 如图,已知矩形ABCD中,R、P分别是DC、BC上的点,E、F分别是AP、RP的中点,当点P在BC上从B向C移动而R不动时,那么下列结论成立的是( )
如图,已知矩形ABCD中,R、P分别是DC、BC上的点,E、F分别是AP、RP的中点,当点P在BC上从B向C移动而R不动时,那么下列结论成立的是( )| A. | 线段EF的长不能确定 | B. | 线段EF的长逐渐增大 | ||
| C. | 线段EF的长逐渐减小 | D. | 线段EF的长不改变 |
| A. | “任意画出一个圆,它是中心对称图形”是随机事件 | |
| B. | 为了解我省中学生的体能情况,应采用普查的方式 | |
| C. | 天气预报明天下雨的概率是99%,说明明天一定会下雨 | |
| D. | 任意掷一枚质地均匀的硬币10次,正面朝上的次数不一定是5次 |
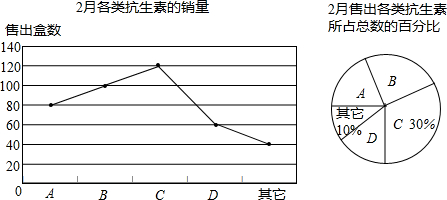
| A | B | C | D | |
| 2月份售价(元/盒) | 15.4 | 8.6 | 11.2 | 28.2 |
| 3月份售价(元/盒) | 12.8 | 7.7 | 10 | 20.5 |
(2)补全扇形统计图;
(3)吴老师到该药房买一些抗生素作为家里备用药,在A、B、C、D各一盒中随机购买两盒,请用画树状图或列表法求出他刚好选中A和B的概率.
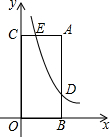 已知,如图,点A($\sqrt{3}$,3),AB⊥x轴于点B,AC⊥y轴于点C,反比例函数y=$\frac{k}{x}$(x>0)的图象与线段AB、AC分别交于D、E.若AB=3BD,则点E的横坐标为$\frac{\sqrt{3}}{3}$.
已知,如图,点A($\sqrt{3}$,3),AB⊥x轴于点B,AC⊥y轴于点C,反比例函数y=$\frac{k}{x}$(x>0)的图象与线段AB、AC分别交于D、E.若AB=3BD,则点E的横坐标为$\frac{\sqrt{3}}{3}$. 如图,四边形OABC是平行四边形,对角线OB在y轴正半轴上,位于第一象限的点A和第二象限的点C分别在双曲线y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$的一支上,分别过点A,C作x轴的垂线,垂足分别为M和N,则有以下结论:
如图,四边形OABC是平行四边形,对角线OB在y轴正半轴上,位于第一象限的点A和第二象限的点C分别在双曲线y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$的一支上,分别过点A,C作x轴的垂线,垂足分别为M和N,则有以下结论: