Question

7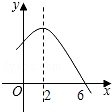．已知二次函数y=-x²+4x+m的部分图象如图所示，则关于x的一元二次方程-x²+4x+m=0的解为x₁=-2，x₂=6．

Answer 1

分析 根据二次函数的图象关于对称轴对称，由题目中给出的图象，可以求得图象与x轴的另一个交点，从而解答本题．

解答 解：∵由函数图象可知二次函数y=-x²+4x+m的对称轴为x=2，与x轴的一个交点为（6，0），
∴二次函数y=-x²+4x+m与x轴的另一个交点的横坐标为：2×2-6=-2．
∴二次函数y=-x²+4x+m与x轴的另一个交点的坐标为：（-2，0）．
∴令y=0，则-x²+4x+m=0得，x₁=-2，x₂=6．
故答案为：x₁=-2，x₂=6．

点评 本题考查抛物线与x轴的交点、抛物线与一元二次方程的关系，解题的关键是能看懂函数的图象，能明确二次函数与一元二次方程的关系．