题目内容
2.a,b,c≠0,且a($\frac{1}{b}$+$\frac{1}{c}$)+b($\frac{1}{c}$+$\frac{1}{a}$)+c($\frac{1}{a}$+$\frac{1}{b}$)=-3,若a,b,c的倒数之和不为0,则a+b+c=0.分析 先将等式右边化为0,再对左边进行因式分解.
解答 解:∵a($\frac{1}{b}$+$\frac{1}{c}$)+b($\frac{1}{c}$+$\frac{1}{a}$)+c($\frac{1}{a}$+$\frac{1}{b}$)=-3,
∴a($\frac{1}{b}$+$\frac{1}{c}$)+b($\frac{1}{c}$+$\frac{1}{a}$)+c($\frac{1}{a}$+$\frac{1}{b}$)+3=0,
∴$\frac{a}{b}+\frac{a}{c}+\frac{b}{a}+\frac{b}{c}+\frac{c}{a}+\frac{c}{b}+\frac{a}{a}+\frac{b}{b}+\frac{c}{c}=0$,
∴$\frac{1}{a}(a+b+c)+\frac{1}{b}(a+b+c)+\frac{1}{c}(a+b+c)=0$,
∴$(a+b+c)(\frac{1}{a}+\frac{1}{b}+\frac{1}{c})=0$,
∵$\frac{1}{a}+\frac{1}{b}+\frac{1}{c}≠0$,
∴a+b+c=0.
点评 此题考查了代数式的恒等变形,将已知等式进行适当的变形变成若干个因式之积等于0的形式是本题的关键.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
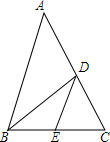 如图,在△ABC中,若$\frac{AB}{AD}$=$\frac{BC}{CD}$,AB=9,BC=6,DE∥AB,则△DCE的面积与四边形ABED的面积比是多少?
如图,在△ABC中,若$\frac{AB}{AD}$=$\frac{BC}{CD}$,AB=9,BC=6,DE∥AB,则△DCE的面积与四边形ABED的面积比是多少?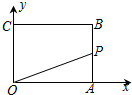 如图,已知矩形OABC,A(4,0),C(0,4),动点P从点A出发,沿A-B-C-O的路线匀速运动,设动点P的运动路程为t,△OAP的面积为S,则下列能大致反映S与t之间关系的图象是( )
如图,已知矩形OABC,A(4,0),C(0,4),动点P从点A出发,沿A-B-C-O的路线匀速运动,设动点P的运动路程为t,△OAP的面积为S,则下列能大致反映S与t之间关系的图象是( )

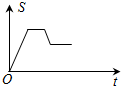
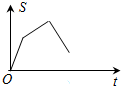
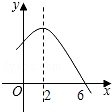 已知二次函数y=-x2+4x+m的部分图象如图所示,则关于x的一元二次方程-x2+4x+m=0的解为x1=-2,x2=6.
已知二次函数y=-x2+4x+m的部分图象如图所示,则关于x的一元二次方程-x2+4x+m=0的解为x1=-2,x2=6.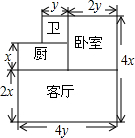 如图是一所住宅的建筑平面图(图中长度单位:m).
如图是一所住宅的建筑平面图(图中长度单位:m).