题目内容
求下列各式中的x:
(1)(x+2)2=16
(2)8(x3+1)=-6.
(1)(x+2)2=16
(2)8(x3+1)=-6.
考点:立方根,平方根
专题:
分析:(1)根据平方根定义开方,即可得出两个一元一次方程,求出方程的解即可;
(3)先去括号,再移项,最后两边都除以8,根据立方根定义求出即可.
(3)先去括号,再移项,最后两边都除以8,根据立方根定义求出即可.
解答:解:(1)(x+2)2=16,
x+2=±4,
x1=2,x2=-6;
(2)8(x3+1)=-6,
8x3=-14,
x3=-
,
x=-
=-
.
x+2=±4,
x1=2,x2=-6;
(2)8(x3+1)=-6,
8x3=-14,
x3=-
| 7 |
| 4 |
x=-
| 3 |
| ||
| |||
| 2 |
点评:本题考查了对平方根和立方根定义的应用,解此题的关键是能转化成一元一次方程,难度不是很大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若关于x的方程kx-3x=24与
=5的解相同,则k的值为( )
| 2x-1 |
| 3 |
| A、8 | B、6 | C、2 | D、0 |
如图图形中,不是轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
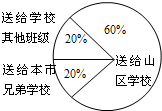 某班同学在“献爱心”活动中捐了图书,捐书的情况如下:每人捐书的册数为:5,10,15,20,相应的捐书人数为:17,22,4,2.根据题目中所给的条件回答下列问题:
某班同学在“献爱心”活动中捐了图书,捐书的情况如下:每人捐书的册数为:5,10,15,20,相应的捐书人数为:17,22,4,2.根据题目中所给的条件回答下列问题: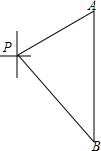 如图,一艘海轮位于灯塔P的北偏东60°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处距离灯塔P有多远?(精确到0.01海里)
如图,一艘海轮位于灯塔P的北偏东60°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处距离灯塔P有多远?(精确到0.01海里)