Question

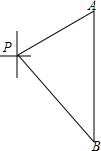如图，一艘海轮位于灯塔P的北偏东60°方向，距离灯塔80海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东45°方向上的B处，这时，海轮所在的B处距离灯塔P有多远？（精确到0.01海里）

Answer 1

考点：解直角三角形的应用-方向角问题

专题：

分析：作PC⊥AB，垂足为C．在Rt△APC中，求出PC的长，再在Rt△PBC中，求出CB的长，将AC和CB相加即可．

解答：解：作PC⊥AB，垂足为C．
∵∠APC=90°-60°=30°，AP=80海里，
∴PC=AP•cos30°=80×

3

2

=40

3

海里，AC=AP•sin30°=80×

1

2

=40海里，
又∵∠BPC=45°，
∴CB=PC=40

3

海里，
∴BP=

2

×40

3

=40

6

（海里）．

点评：本题考查了解直角三角形的应用--方向角问题，结合航海中的实际问题，将解直角三角形的相关知识有机结合，体现了数学应用于实际生活的思想．