题目内容
如图，已知弦CD⊥直径AB于E，CD=2
，BD=
，求直径AB的长．
| 2 |
| 3 |
连接OC，
∵CD⊥AB，
∴E为CD的中点，即CE=DE=
CD=
，
在Rt△BDE中，BD=
，DE=
，
根据勾股定理得：EB=
=1，
设半径OC=OB=r，则OE=OB-EB=r-1，
在Rt△COE中，OC=r，CE=
，OE=r-1，
根据勾股定理得：r2=（
）2+（r-1）2，
解得：r=
，
则直径AB为3．
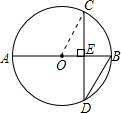
∵CD⊥AB，
∴E为CD的中点，即CE=DE=
| 1 |
| 2 |
| 2 |
在Rt△BDE中，BD=
| 3 |
| 2 |
根据勾股定理得：EB=
| BD2-ED2 |
设半径OC=OB=r，则OE=OB-EB=r-1，
在Rt△COE中，OC=r，CE=
| 2 |
根据勾股定理得：r2=（
| 2 |
解得：r=
| 3 |
| 2 |
则直径AB为3．
练习册系列答案
同步奥数系列答案
相关题目
