题目内容
以点M(3,0)为圆心,5为半径作圆,与坐标轴交于点A,B,C,D,求点A,B,C,D的坐标.
考点:坐标与图形性质
专题:
分析:设圆与x轴交于点A,B,与y轴交于点C,D.因为是点M(3,0)为圆心,5为半径作圆,圆心在x轴上,所以将点M分别向左、向右平移5个单位得到与x轴交点A,B的坐标;连结MC,在Rt△OMC中,利用勾股定理求出OC=
=4,得到C点坐标,同理求出D点坐标.
| MC2-OM2 |
解答: 解:如图,以点M(3,0)为圆心,5为半径作圆,设与x轴交于点A,B,与y轴交于点C,D.
解:如图,以点M(3,0)为圆心,5为半径作圆,设与x轴交于点A,B,与y轴交于点C,D.
∵MA=MB=5,M(3,0),
∴A点坐标为(3-5,0),B点坐标为(3+5,0),
即A(-2,0),B(8,0).
连结MC.
在Rt△OMC中,∵∠MOC=90°,OM=3,MC=5,
∴OC=
=
=4,
∴C点坐标为(0,-4),
同理求出D点坐标为(0,4).
 解:如图,以点M(3,0)为圆心,5为半径作圆,设与x轴交于点A,B,与y轴交于点C,D.
解:如图,以点M(3,0)为圆心,5为半径作圆,设与x轴交于点A,B,与y轴交于点C,D.∵MA=MB=5,M(3,0),
∴A点坐标为(3-5,0),B点坐标为(3+5,0),
即A(-2,0),B(8,0).
连结MC.
在Rt△OMC中,∵∠MOC=90°,OM=3,MC=5,
∴OC=
| MC2-OM2 |
| 52-32 |
∴C点坐标为(0,-4),
同理求出D点坐标为(0,4).
点评:本题考查了坐标与图形性质,勾股定理,属于基础题,做此类题最好先根据题意画出图形,便于解答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
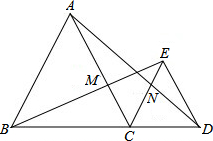 如图,△ABC与△CDE都是等边三角形,点B,C,D在同一直线上,BE与AC交于点M,AD与EC交于点N.
如图,△ABC与△CDE都是等边三角形,点B,C,D在同一直线上,BE与AC交于点M,AD与EC交于点N.