题目内容
13．已知x=1是一元二次方程ax2+bx-10=0的一个根，则分式$\frac{{a}^{2}+2ab+{b}^{2}}{2a+2b}$的值为5．分析 根据一元二次方程解的定义把x=1代入ax2+bx-10=0即可得到a+b的值．
解答 解：把x=1代入方程ax2+bx-10=得a+b-10=0，
解a+b=10．
$\frac{{a}^{2}+2ab+{b}^{2}}{2a+2b}$=$\frac{（a+b）^{2}}{2（a+b）}$=$\frac{a+b}{2}$=5
故答案为5．
点评 本题考查了一元二次方程的解：能使一元二次方程左右两边相等的未知数的值是一元二次方程的解．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
4．
实数a，b在数轴上的位置如图所示，以下说法正确的是（ ）
实数a，b在数轴上的位置如图所示，以下说法正确的是（ ）| A． | a+b=0 | B． | ab＞0 | C． | b＜a | D． | |b|＜|a| |
8．
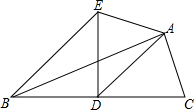如图，AD是△ABC的中线，∠ADC=45°，把△ABC沿着直线AD对折，点C落在点E的位置，如果BC=12，那么线段BE的长度为（ ）
如图，AD是△ABC的中线，∠ADC=45°，把△ABC沿着直线AD对折，点C落在点E的位置，如果BC=12，那么线段BE的长度为（ ）| A． | 12 | B． | 12$\sqrt{2}$ | C． | 6$\sqrt{2}$ | D． | 4$\sqrt{3}$ |
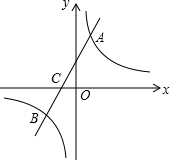如图，在平面直角坐标系中，一次函数y=kx+b（k≠0）的图象与反比例函数y=$\frac{m}{x}$（m≠0）的图象交于A，B两点，与x轴交于C点，已知点A的坐标为（n，6），点C的坐标为（-2，0），且tan∠ACO=2．