Question

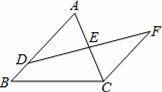
如图，D是△ABC的边AB上一点，E是AC的中点，过点C作CF∥AB，交DE的延长线于点F．求证：AB=CF+BD．

Answer 1

【考点】全等三角形的判定与性质．

【专题】证明题．

【分析】根据平行线性质得出∠ADE=∠F，∠ECF=∠A，求出AE=EC，根据AAS证△ADE≌△CFE，根据全等三角形的性质推出AD=CF，即可解答．

【解答】解：∵E是AC的中点，

∴AE=CE． 

∵CF∥AB，

∴∠A=∠ECF，∠ADE=∠F，

在△ADE与△CFE中，

，

∴△ADE≌△CFE（AAS）．

∴AD=CF． 

∴AD+BD=CF+BD=AB．

【点评】本题考查了全等三角形的性质和判定，平行线的性质，注意：全等三角形的对应边相等，全等三角形的判定定理有SAS，ASA，AAS，SSS．