题目内容
如图,已知AB是⊙O的直径,且AB=12,AP是半圆的切线,点C是半圆上的一动点(不与点A、B重合),过点C作CD⊥AP于点D,记∠COA=α.
(1)当α=60°时,求CD的长;
(2)当α为何值时,CD与⊙O相切?说明理由;
(3)当AD=3
时,求α的值.
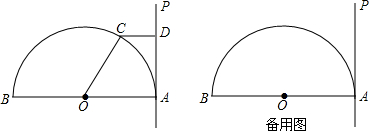
(1)当α=60°时,求CD的长;
(2)当α为何值时,CD与⊙O相切?说明理由;
(3)当AD=3
| 2 |

考点:切线的判定与性质
专题:
分析:(1)作CE⊥AB于点E,在直角△OCE中,利用三角函数求得OE的长,则CD=AE=OA-OE,据此即可求解;
(2)当∠α=90°时,CD与⊙O相切,根据切线的性质以及矩形的判定定理即可作出判断;
(3)在直角△OCE中,利用三角函数求得∠COE的度数,即可求得∠α的度数.
(2)当∠α=90°时,CD与⊙O相切,根据切线的性质以及矩形的判定定理即可作出判断;
(3)在直角△OCE中,利用三角函数求得∠COE的度数,即可求得∠α的度数.
解答:解:(1)作CE⊥AB于点E.
在直角△OCE中,OE=OC•cos∠COA=
×6=3,
则CD=OA-OE=6-3=3;
(2)∠α=90°,CD与⊙O相切.
理由:当∠α=90°,
则在四边形OCDA中,∠COA=∠OAD=∠CDA=90°,
∴∠OCD=90°,
∴OC⊥CD,
∴CD是⊙O的切线;
(3)当 C的位置如左边的图时,在直角△OCE中,OC=6,CE=AD=3
C的位置如左边的图时,在直角△OCE中,OC=6,CE=AD=3
,
∴sin∠COE=
=
,
∴∠COE=45°,
则∠α=45°,
当C的位置如右图时,∠COE=45°,
则∠α=180°-45°=135°.
故α=45°或α=135°.
在直角△OCE中,OE=OC•cos∠COA=
| 1 |
| 2 |
则CD=OA-OE=6-3=3;
(2)∠α=90°,CD与⊙O相切.
理由:当∠α=90°,
则在四边形OCDA中,∠COA=∠OAD=∠CDA=90°,
∴∠OCD=90°,
∴OC⊥CD,
∴CD是⊙O的切线;
(3)当
 C的位置如左边的图时,在直角△OCE中,OC=6,CE=AD=3
C的位置如左边的图时,在直角△OCE中,OC=6,CE=AD=3| 2 |
∴sin∠COE=
3
| ||
| 6 |
| ||
| 2 |
∴∠COE=45°,
则∠α=45°,
当C的位置如右图时,∠COE=45°,
则∠α=180°-45°=135°.
故α=45°或α=135°.
点评:本题考查了三角函数以及切线的判定方法,正确对C的位置分成两种情况进行讨论是关键.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
 如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AC平分∠DAB.
如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AC平分∠DAB. 如图,以?ABCD的边AB为直径的⊙O经过点D,点E在⊙O上,∠AED=45°,
如图,以?ABCD的边AB为直径的⊙O经过点D,点E在⊙O上,∠AED=45°, 为了解某校九年级女生1分钟仰卧起坐的次数,从中随机抽查了50名女生参加测试,被抽查的女生中有90%的女生次数不小于30次,并绘制成频数分布直方图(如图),那么仰卧起坐的次数在40~45的频率是
为了解某校九年级女生1分钟仰卧起坐的次数,从中随机抽查了50名女生参加测试,被抽查的女生中有90%的女生次数不小于30次,并绘制成频数分布直方图(如图),那么仰卧起坐的次数在40~45的频率是