题目内容
17.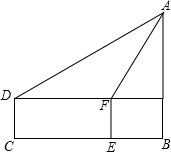 小丽为了测旗杆AB的高度,小丽眼睛距地面1.5米,小丽站在C点,测出旗杆A的仰角为30°,小丽向前走了10米到达点E,此时的仰角为60°,求旗杆的高度.
小丽为了测旗杆AB的高度,小丽眼睛距地面1.5米,小丽站在C点,测出旗杆A的仰角为30°,小丽向前走了10米到达点E,此时的仰角为60°,求旗杆的高度.
分析 关键三角形外角的性质求得∠DAF=30°,得出AF=DF=10,在Rt△FGA中,根据正弦函数求出AG的长,加上BG的长即为旗杆高度.
解答  解:如图,∵∠ADG=30°,∠AFG=60°,
解:如图,∵∠ADG=30°,∠AFG=60°,
∴∠DAF=30°,
∴AF=DF=10,
在Rt△FGA中,
AG=AF•sin∠AFG=10×$\frac{\sqrt{3}}{2}$=5$\sqrt{3}$,
∴AB=1.5+5$\sqrt{3}$.
答:旗杆AB的高度为(1.5+5$\sqrt{3}$)米.
点评 本题考查了解直角三角形的应用--仰角俯角问题,要求学生能借助仰角构造直角三角形并解直角三角形.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
8.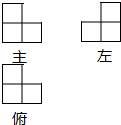 由若干个边长为1cm的正方体堆积成一个几何体,它的三视图如图,则这个几何体的表面积是( )
由若干个边长为1cm的正方体堆积成一个几何体,它的三视图如图,则这个几何体的表面积是( )
 由若干个边长为1cm的正方体堆积成一个几何体,它的三视图如图,则这个几何体的表面积是( )
由若干个边长为1cm的正方体堆积成一个几何体,它的三视图如图,则这个几何体的表面积是( )| A. | 15cm2 | B. | 18cm2 | C. | 21cm2 | D. | 24cm2 |
5.若用一张直径为20cm的半圆形铁片做一个圆锥的侧面,接缝忽略不计,则所得圆锥的高为( )
| A. | 5$\sqrt{3}$cm | B. | 5$\sqrt{5}$cm | C. | $\frac{5\sqrt{15}}{2}$cm | D. | 10cm |
12. 下列主视图正确的是( )
下列主视图正确的是( )
 下列主视图正确的是( )
下列主视图正确的是( )| A. |  | B. |  | C. |  | D. |  |
9. 如图所示物体的主视图是( )
如图所示物体的主视图是( )
 如图所示物体的主视图是( )
如图所示物体的主视图是( )| A. |  | B. |  | C. |  | D. |  |
6.计算-3+(-1)的结果是( )
| A. | 2 | B. | -2 | C. | 4 | D. | -4 |
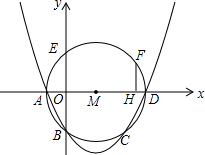 如图,在平面直角坐标系中,抛物线y=ax2+bx+c与⊙M相交于A、B、C、D四点,其中A、B两点的坐标分别为(-1,0),(0,-2),点D在x轴上且AD为⊙M的直径.点E是⊙M与y轴的另一个交点,过劣弧$\widehat{ED}$上的点F作FH⊥AD于点H,且FH=1.5
如图,在平面直角坐标系中,抛物线y=ax2+bx+c与⊙M相交于A、B、C、D四点,其中A、B两点的坐标分别为(-1,0),(0,-2),点D在x轴上且AD为⊙M的直径.点E是⊙M与y轴的另一个交点,过劣弧$\widehat{ED}$上的点F作FH⊥AD于点H,且FH=1.5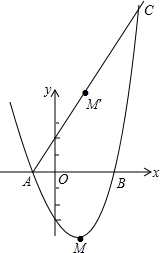 如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点,顶点M关于x轴的对称点是M′.
如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点,顶点M关于x轴的对称点是M′.