题目内容
18.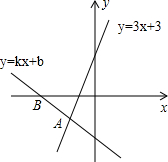 如图,经过点B(-3,0)的直线y=kx+b与直线y=3x+3相交于点A(-2,-3),则不等式3x+3<kx+b<0的解集为-3<x<-2.
如图,经过点B(-3,0)的直线y=kx+b与直线y=3x+3相交于点A(-2,-3),则不等式3x+3<kx+b<0的解集为-3<x<-2.
分析 由图象得到直线y=kx+b与直线y=4x+2的交点A的坐标(-2,-3)及直线y=kx+b与x轴的交点坐标,观察直线y=3x+3落在直线y=kx+b的下方且直线y=kx+b落在x轴下方的部分对应的x的取值即为所求.
解答 解:∵经过点B(-3,0)的直线y=kx+b与直线y=3x+3相交于点A(-2,-3),
∴直线y=kx+b与直线y=3x+3的交点A的坐标为(-2,-3),直线y=kx+b与x轴的交点坐标为B(-3,0),
又∵当x<-2时,3x+3<kx+b,
当x>-3时,kx+b<0,
∴不等式3x+3<kx+b<0的解集为-3<x<-2.
故答案为-3<x<-2.
点评 本题考查了一次函数与一元一次不等式的关系:从函数的角度看,就是寻求使一次函数y=ax+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.下列方程中,以x=2为解的是( )
| A. | 2x=3 | B. | 2x+1=3 | C. | 5x=10 | D. | 3x+1=4 |
13.有一个袋子里装有6个红球,5个白球,1个黑球,每个球除了颜色外,其他都相同,任意摸出一个球,则最有可能摸到的是( )
| A. | 红球 | B. | 白球 | C. | 黑球 | D. | 无法确定 |
3.下列运算正确的是( )
| A. | (-1)3+(-1)2=0 | B. | 1-2×32=-9 | C. | (a+b)2=a2+b2 | D. | (a2)3=a5 |
10.计算(a2)3的结果是( )
| A. | a5 | B. | a6 | C. | a8 | D. | 3 a2 |
7.在1,0,2,-3这四个数中,负数是( )
| A. | 1 | B. | 0 | C. | 2 | D. | -3 |
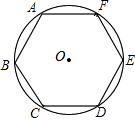 如图,正六边形ABCDEF内接于⊙O,向⊙O内任意投点,则所投的点落在正六边形ABCDEF内的概率是$\frac{3\sqrt{3}}{2π}$.
如图,正六边形ABCDEF内接于⊙O,向⊙O内任意投点,则所投的点落在正六边形ABCDEF内的概率是$\frac{3\sqrt{3}}{2π}$.