题目内容
9.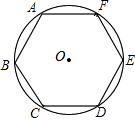 如图,正六边形ABCDEF内接于⊙O,向⊙O内任意投点,则所投的点落在正六边形ABCDEF内的概率是$\frac{3\sqrt{3}}{2π}$.
如图,正六边形ABCDEF内接于⊙O,向⊙O内任意投点,则所投的点落在正六边形ABCDEF内的概率是$\frac{3\sqrt{3}}{2π}$.
分析 连接OE、OD,由正六边形的特点求出判断出△ODE的形状,作OH⊥ED于H,由特殊角的三角函数值求出OH的长,利用三角形的面积公式即可求出△ODE的面积,进而可得出正六边形ABCDEF的面积,即可得出结果.
解答 解:设⊙O的半径为R,连接OE、OD,如图所示: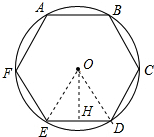
∵六边形ABCDEF是正六边形,
∴∠DEF=120°,
∴∠OED=60°,
∵OE=OD=R,
∴△ODE是等边三角形,
∴DE=OD=R,
作OH⊥ED于H,则OH=OE•sin∠OED=R×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$R,
∴S△ODE=$\frac{1}{2}$DE•OH=$\frac{1}{2}$×R×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{4}$R2,
∴正六边形的面积=6×$\frac{\sqrt{3}}{4}$R2=$\frac{3\sqrt{3}}{2}$R2,
∵⊙O的面积=πR2,
∴所投的点落在正六边形ABCDEF内的概率=$\frac{\frac{3\sqrt{3}}{2}{R}^{2}}{π{R}^{2}}$=$\frac{3\sqrt{3}}{2π}$.
故答案为:$\frac{3\sqrt{3}}{2π}$.
点评 本题考查的是正多边形和圆、正六边形的性质、等边三角形的判定与性质、三角函数;熟练掌握正六边形的性质,通过作辅助线求出△ODE的面积是解决问题的关键.

练习册系列答案
相关题目
19.已知实数a、b满足(a2-b2)2-2(a2-b2)=8,则a2-b2的值为( )
| A. | -2 | B. | 4 | C. | 4或-2 | D. | -4或2 |
20.在⊙O中,⊙O的半径为6cm,弦AB的长为6cm,则弦AB所对的圆周角是( )
| A. | 60°或120° | B. | 30°或150° | C. | 60° | D. | 30° |
17.下列变形中,不正确的是( )
| A. | 若x=y,则5+x=5+y | B. | 若-$\frac{x}{5}$=-$\frac{y}{5}$,则x=y | ||
| C. | 若mx=my,则x=y | D. | 若x=y,则2x-3=2y-3 |
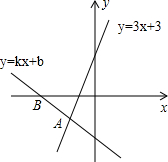 如图,经过点B(-3,0)的直线y=kx+b与直线y=3x+3相交于点A(-2,-3),则不等式3x+3<kx+b<0的解集为-3<x<-2.
如图,经过点B(-3,0)的直线y=kx+b与直线y=3x+3相交于点A(-2,-3),则不等式3x+3<kx+b<0的解集为-3<x<-2.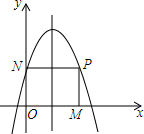 如图,抛物线的顶点坐标为(2,6),且经过点(4,2).P是抛物线上x轴上方一点,且在对称轴右侧,过点P作PM⊥x轴于点M,PN⊥y轴于点N.设点P横坐标为m.
如图,抛物线的顶点坐标为(2,6),且经过点(4,2).P是抛物线上x轴上方一点,且在对称轴右侧,过点P作PM⊥x轴于点M,PN⊥y轴于点N.设点P横坐标为m.