题目内容
6.已知一次函数y=kx+b,当0≤x≤2时,对应的函数值y的取值范围是-2≤y≤4,则kb的值为-6或-12.分析 由一次函数的性质,分k>0和k<0时两种情况讨论求解.
解答 解:(1)当k>0时,y随x的增大而增大,即一次函数为增函数,
∴当x=0时,y=-2,当x=2时,y=4,
代入一次函数解析式y=kx+b得:$\left\{\begin{array}{l}{b=-2}\\{2k+b=4}\end{array}\right.$
解得$\left\{\begin{array}{l}{k=3}\\{b=-2}\end{array}\right.$,
∴kb=3×(-2)=-6;
(2)当k<0时,y随x的增大而减小,即一次函数为减函数,
∴当x=0时,y=4,当x=2时,y=-2,
代入一次函数解析式y=kx+b得:$\left\{\begin{array}{l}{b=4}\\{2k+b=-2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-3}\\{b=4}\end{array}\right.$
∴kb=-3×4=-12.
所以kb的值为-6或-12.
点评 此题考查一次函数的性质,要注意根据一次函数图象的性质要分情况讨论.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
17.下列变形中,不正确的是( )
| A. | 若x=y,则5+x=5+y | B. | 若-$\frac{x}{5}$=-$\frac{y}{5}$,则x=y | ||
| C. | 若mx=my,则x=y | D. | 若x=y,则2x-3=2y-3 |
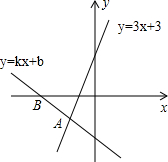 如图,经过点B(-3,0)的直线y=kx+b与直线y=3x+3相交于点A(-2,-3),则不等式3x+3<kx+b<0的解集为-3<x<-2.
如图,经过点B(-3,0)的直线y=kx+b与直线y=3x+3相交于点A(-2,-3),则不等式3x+3<kx+b<0的解集为-3<x<-2. 如图,Rt△ABC中,∠C=90°,∠B=30°,AD是∠BAC的平分线,AD=10,则点D到AB的距离是( )
如图,Rt△ABC中,∠C=90°,∠B=30°,AD是∠BAC的平分线,AD=10,则点D到AB的距离是( )