题目内容
如图，在等边三角形△ABC中，D点在BC上，且∠CAD=15°，则| CD |
| BD |
考点：解直角三角形,等边三角形的性质,含30度角的直角三角形
专题：
分析：过点D作DM⊥AB于点M，借助于各角度数表示出CD，BD的长，进而求出即可．
解答：
解：过点D作DM⊥AB于点M，
∵在等边三角形△ABC中，D点在BC上，且∠CAD=15°，
∴∠B=60°，∠BAD=45°，
∴AM=MD，∠BDM=30°，
∴设BM=x，则BD=2x，
故DM=
x，
∴BC=AB=x+
x，
∴
=
=
．
故答案为：
．
解：过点D作DM⊥AB于点M，∵在等边三角形△ABC中，D点在BC上，且∠CAD=15°，
∴∠B=60°，∠BAD=45°，
∴AM=MD，∠BDM=30°，
∴设BM=x，则BD=2x，
故DM=
| 3 |
∴BC=AB=x+
| 3 |
∴
| CD |
| BD |
x+
| ||
| 2x |
| ||
| 2 |
故答案为：
| ||
| 2 |
点评：此题主要考查了解直角三角形，等边三角形的性质，以及含30度角的直角三角形的性质等知识，表示出DC的长是解题关键．
练习册系列答案
冲刺100分单元优化练考卷系列答案
相关题目
如图，已知函数y=ax-b和y=cx+d的图象交于点P，根据图象可得方程组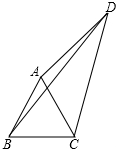
如图，四边形ABCD中，AC，BD是对角线，△ABC是等边三角形，∠ADC=30°，AD=3，BD=5，则四边形ABCD的面积为