题目内容
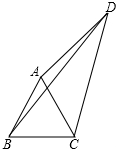 如图,四边形ABCD中,AC,BD是对角线,△ABC是等边三角形,∠ADC=30°,AD=3,BD=5,则四边形ABCD的面积为
如图,四边形ABCD中,AC,BD是对角线,△ABC是等边三角形,∠ADC=30°,AD=3,BD=5,则四边形ABCD的面积为考点:旋转的性质,全等三角形的判定与性质,勾股定理
专题:
分析:以AD为边作正△ADE,根据等边三角形的性质可得AB=AC,AD=AE,∠BAC=∠DAE=60°,再求出∠BAD=∠CAE,然后利用“边角边”证明△ABD和△ACE全等,根据全等三角形对应边相等可得CE=BD,然后求出∠CDE=90°,再利用勾股定理列式求出CD=4,过点A作AF⊥CD于F,根据直角三角形30°角所对的直角边等于斜边的一半可得AF=
AD,利用勾股定理列式求DF,再求出CF,然后利用勾股定理列式求出AC2,然后根据S四边形ABCD=S△ABC+S△ACD列式计算即可得解.
| 1 |
| 2 |
解答:解:如图,以AD为边作正△ADE,
∵△ABC也是等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=60°,
∵∠BAD=∠BAC+∠CAD,
∠CAE=∠DAE+∠CAD,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴CE=BD=5,
∵∠CDE=∠ADE+∠ADC=60°+30°=90°,
∴CD=
=
=4,
过点A作AF⊥CD于F,∵∠ADC=30°,
∴AF=
AD=
,
由勾股定理得,DF=
=
,
∴CF=CD-DF=4-
,
在Rt△ACF中,AC2=AF2+CF2=(
)2+(4-
)2=25-12
,
所以S四边形ABCD=S△ABC+S△ACD
=
×
×(25-12
)+
×4×
=
-9+3
=
.
故答案为:
.
∵△ABC也是等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=60°,
∵∠BAD=∠BAC+∠CAD,

∠CAE=∠DAE+∠CAD,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
|
∴△ABD≌△ACE(SAS),
∴CE=BD=5,
∵∠CDE=∠ADE+∠ADC=60°+30°=90°,
∴CD=
| CE2-DE2 |
| 52-32 |
过点A作AF⊥CD于F,∵∠ADC=30°,
∴AF=
| 1 |
| 2 |
| 3 |
| 2 |
由勾股定理得,DF=
32-(
|
3
| ||
| 2 |
∴CF=CD-DF=4-
3
| ||
| 2 |
在Rt△ACF中,AC2=AF2+CF2=(
| 3 |
| 2 |
3
| ||
| 2 |
| 3 |
所以S四边形ABCD=S△ABC+S△ACD
=
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
=
25
| ||
| 4 |
=
25
| ||
| 4 |
故答案为:
25
| ||
| 4 |
点评:本题考查了旋转的性质,等边三角形的性质,全等三角形的判定与性质,勾股定理,难点在于作辅助线构造出等边三角形和全等三角形.

练习册系列答案
相关题目
 如图,是一个正方体的展开图,若原正方体朝上的面上的字是“祝”,则与其相对的朝下的面上的字应是( )
如图,是一个正方体的展开图,若原正方体朝上的面上的字是“祝”,则与其相对的朝下的面上的字应是( )| A、考 | B、试 | C、顺 | D、利 |
下列运算正确的是( )
| A、-22=4 | ||||
B、(-
| ||||
| C、(-2)2=-4 | ||||
| D、(-2)3=-6 |
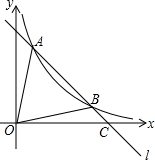 如图,直线l与反比例函数y=
如图,直线l与反比例函数y=| 2 |
| x |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,在等边三角形△ABC中,D点在BC上,且∠CAD=15°,则
如图,在等边三角形△ABC中,D点在BC上,且∠CAD=15°,则