题目内容
14.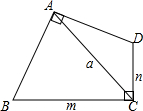 如图,四边形ABCD中,∠A=∠C=90°,AB=AD,BC=m,CD=n,对角线AC=a,则m,n,a满足的数量关系是m+n=$\sqrt{2}$a.
如图,四边形ABCD中,∠A=∠C=90°,AB=AD,BC=m,CD=n,对角线AC=a,则m,n,a满足的数量关系是m+n=$\sqrt{2}$a.
分析 如图,延长CB到M,使得BM=CD,连接AM.由△ABM≌△ADC,推出△MAC是等腰直角三角形,即可解决问题.
解答 解:如图,延长CB到M,使得BM=CD,连接AM.
∵∠BAD=90°,∠BCD=90°,
∴∠BAD+∠BCD=180°,
∴∠ABC+∠D=180°,∵∠ABC+∠ABM=180°,
∴∠ABM=∠D,
在△ABM和△ADC中,
$\left\{\begin{array}{l}{BM=CD}\\{∠ABM=∠D}\\{AB=AD}\end{array}\right.$,
∴△ABM≌△ADC,
∴AM=AC=a,∠BAM=∠CAD,
∴∠MAC=∠BAD=90°,
∴△MAC是等腰直角三角形,
∴MC=$\sqrt{2}$AM,
∴BM+BC=$\sqrt{2}$AC,
∴m+n=$\sqrt{2}$a.
故答案为m+n=$\sqrt{2}$a.
点评 本题考查全等三角形 的判定和性质、等腰直角三角形的判定和性质等知识,解题的关键是学会利用旋转法添加辅助线,构造全等三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
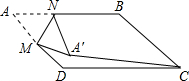 如图,?ABCD中,AB=2$\sqrt{2}$,BC=2,∠B=135°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是$\sqrt{13}$-1.
如图,?ABCD中,AB=2$\sqrt{2}$,BC=2,∠B=135°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是$\sqrt{13}$-1.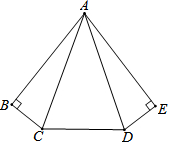 已知五边形ABCDE中,∠B=∠E=90°,AB=AE,AC=AD,∠BCD=140°.
已知五边形ABCDE中,∠B=∠E=90°,AB=AE,AC=AD,∠BCD=140°.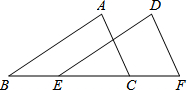 如图,△ABC≌△DEF,∠A和∠D是对应角,AB和DE是对应边,那么还有对应角是∠B=∠E,∠C=∠F,对应边是BC=EF,AC=DF.
如图,△ABC≌△DEF,∠A和∠D是对应角,AB和DE是对应边,那么还有对应角是∠B=∠E,∠C=∠F,对应边是BC=EF,AC=DF.