题目内容
3.已知y1=mx(m≠0),y2=$\frac{k}{x}$(k≠0),当x=1时,y1=y2,当x=2时,y1=y2+9,当x=3时,y1-y2值为( )| A. | 3 | B. | 12 | C. | 16 | D. | 21 |
分析 先利用当x=1时,y1=y2,当x=2时,y1=y2+9得到$\left\{\begin{array}{l}{m=k}\\{2m=\frac{k}{2}+9}\end{array}\right.$,再解关于k、m的方程组确定反比例函数和一次函数解析式,然后计算自变量为3时两个对应的函数值之差.
解答 解:根据题意得$\left\{\begin{array}{l}{m=k}\\{2m=\frac{k}{2}+9}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=6}\\{k=6}\end{array}\right.$,
所以y1=6x,y2=$\frac{6}{x}$,
所以x=3时,y1-y2=3×6-$\frac{6}{3}$=16.
故选C.
点评 本题考查了待定系数法求反比例函数的解析式:设出含有待定系数的反比例函数解析式y=xk(k为常数,k≠0);把已知条件(自变量与函数的对应值)带入解析式,得到待定系数的方程;解方程,求出待定系数;写出解析式.也考查了待定系数法求一次函数解析式.

练习册系列答案
相关题目
14.下列函数中,自变量的取值范围是x≥2的是( )
| A. | y=x-2 | B. | $y=\frac{1}{x-2}$ | C. | $y=\sqrt{x-2}$ | D. | $y=\frac{1}{{\sqrt{x-2}}}$ |
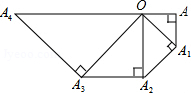 如图,在等腰Rt△OAA1中,∠OAA1=90°,OA=1,以OA1为直角边作等腰Rt△OA1A2,以OA2为直角边作等腰Rt△OA2A3,…,则OAn的长度为$\sqrt{{2}^{n}}$.
如图,在等腰Rt△OAA1中,∠OAA1=90°,OA=1,以OA1为直角边作等腰Rt△OA1A2,以OA2为直角边作等腰Rt△OA2A3,…,则OAn的长度为$\sqrt{{2}^{n}}$.
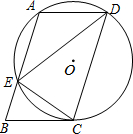 如图,在?ABCD中,过A、C、D三点的⊙O交AB于点E,连接DE、CE,∠CDE=∠BCE.
如图,在?ABCD中,过A、C、D三点的⊙O交AB于点E,连接DE、CE,∠CDE=∠BCE.