题目内容
15．解方程组：$\left\{\begin{array}{l}3x+y=5\\ x-2y=4\end{array}\right.$．分析 方程组利用加减消元法求出解即可．
解答 解：$\left\{\begin{array}{l}{3x+y=5①}\\{x-2y=4②}\end{array}\right.$，
①×2+②得：7x=14，即x=2，
把x=2代入②得：y=-1，
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$．
点评 此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．
练习册系列答案
相关题目
5．关于x的一元二次方程mx2-2x-1=0有两个实数根，那么字母m的取值范围是（ ）
| A． | m≥-1 | B． | m＞-1 | C． | m≥-1且m≠0 | D． | m＞-1且m≠0 |
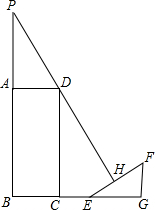如图，一侧面为矩形的建筑物ABCD，AP为建筑物上一灯杆（垂直于地面），夜晚灯杆顶端灯亮时，EH段是建筑物在斜坡EF上的影子．己知BC=8米，AP=12米，CE=6米，斜坡EF的坡角∠FEG=30°，EH=4米，且B，C，E，G在同一水平线上，题中涉及的各点均在同一平面内，求建筑物的高度AB（结果保留根号）．
10．函数$y=\sqrt{x-1}$中，自变量x的取值范围是（ ）
| A． | 全体实数 | B． | x≠1 | C． | x＞1 | D． | x≥1 |
20．下列计算中，正确的是（ ）
| A． | 2a2+3a2=5a4 | B． | （a-b）2=a2-b2 | C． | （a3）3=a6 | D． | （-2a2）3=-8a6 |
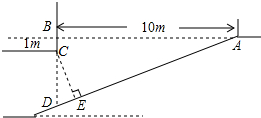近年来，有私家车的业主越来越多，某小区为解决“停车难”问题，拟建造一个地下停车库．如图是该地下停车库坡道入口的设计示意图，其中水平线AB=10m，BD⊥AB，∠BAD=20°，点C在BD上，BC=1m．根据规定，地下停车库坡道入口上方要张贴限高标志，以提醒驾驶员所驾车辆能否安全驶入．李建认为CD的长度就是限制的高度，而孙杰认为应该以CE的长度作为限制的高度．李建和孙杰谁说的对？请你判断并计算出限制高度．（结果精确到0.1m，参考数据：sin20°≈0.34，cos20°≈0.94，tan20°≈0.36）
10．在第二象限内，到x轴距离为3，到y轴距离为2的点P坐标为（ ）
| A． | （3，2） | B． | （2，3） | C． | （-3，2） | D． | （-2，3） |