题目内容
 已知:如图,反比例函数y=
已知:如图,反比例函数y=| k |
| x |
(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量x的取值范围.
考点:反比例函数与一次函数的交点问题
专题:代数几何综合题
分析:(1)把A的坐标代入反比例函数解析式求出A的坐标,把A的坐标代入一次函数解析式求出即可;
(2)求出直线AB与y轴的交点C的坐标,分别求出△ACO和△BOC的面积,然后相加即可;
(3)根据A、B的坐标结合图象即可得出答案.
(2)求出直线AB与y轴的交点C的坐标,分别求出△ACO和△BOC的面积,然后相加即可;
(3)根据A、B的坐标结合图象即可得出答案.
解答:解:(1)把A点(1,4)分别代入反比例函数y=
,一次函数y=x+b,得k=1×4,1+b=4,
解得k=4,b=3,
∴反比例函数的解析式是y=
,一次函数解析式是y=x+3;
(2)如图, 设直线y=x+3与y轴的交点为C,
设直线y=x+3与y轴的交点为C,
当x=-4时,y=-1,
∴B(-4,-1),
当x=0时,y=3,
∴C(0,3),
∴S△AOB=S△AOC+S△BOC=
×3×4+
×3×1=
;
(3)∵B(-4,-1),A(1,4),
∴根据图象可知:当x>1或-4<x<0时,一次函数值大于反比例函数值.
| k |
| x |
解得k=4,b=3,
∴反比例函数的解析式是y=
| 4 |
| x |
(2)如图,
 设直线y=x+3与y轴的交点为C,
设直线y=x+3与y轴的交点为C,当x=-4时,y=-1,
∴B(-4,-1),
当x=0时,y=3,
∴C(0,3),
∴S△AOB=S△AOC+S△BOC=
| 1 |
| 2 |
| 1 |
| 2 |
| 15 |
| 2 |
(3)∵B(-4,-1),A(1,4),
∴根据图象可知:当x>1或-4<x<0时,一次函数值大于反比例函数值.
点评:本题考查了一次函数和反比例函数的交点问题,用待定系数法求出一次函数的解析式,三角形的面积,一次函数的图象等知识点,题目具有一定的代表性,是一道比较好的题目,用了数形结合思想.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案
相关题目

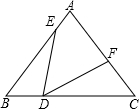 如图,△ABC,AB=AC=10,BC=12,点D在边BC,且BD=4,以点D为顶点作∠EDF=∠B,分别交边AB于点E,交射线CA于点F
如图,△ABC,AB=AC=10,BC=12,点D在边BC,且BD=4,以点D为顶点作∠EDF=∠B,分别交边AB于点E,交射线CA于点F
