题目内容
 如图,有一座圆形拱桥,其跨度AB=8m,拱高CD=2m,则弧AB所在圆的半径为( )?
如图,有一座圆形拱桥,其跨度AB=8m,拱高CD=2m,则弧AB所在圆的半径为( )?| A、5m | B、4m | C、3m | D、2m |
考点:垂径定理的应用,勾股定理
专题:
分析:先根据题意找出圆心,连接OA,OD,由垂径定理得出AB=2AD,再根据拱的半径为13米,拱高CD为8米求出OD的长,根据勾股定理即可得出AD的长,进而得出结论.
解答: 解:如图所示,连接OA,OD,
解:如图所示,连接OA,OD,
∵AB⊥CD,
∴AB=2AD,
∵AB=8m,CD=2m,
∴AD=4m,
设OA=r,则OD=r-2,
在Rt△AOD中,
∵OA2=AD2+OD2,即r2=42+(r-2)2,解得r=5m.
故选A.
 解:如图所示,连接OA,OD,
解:如图所示,连接OA,OD,∵AB⊥CD,
∴AB=2AD,
∵AB=8m,CD=2m,
∴AD=4m,
设OA=r,则OD=r-2,
在Rt△AOD中,
∵OA2=AD2+OD2,即r2=42+(r-2)2,解得r=5m.
故选A.
点评:本题主要考查直角三角形和垂径定理的应用,根据题意作出辅助线是解答此题的关键.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
在Rt△ABC中,∠C=90°,AB=3,AC=2,则cosB=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在-
,-|-6|,-(-5),-32,(-1)2,20%,0这七个数中,正数的个数有( )
| 2 |
| 3 |
| A、5个 | B、4个 | C、3个 | D、2个 |
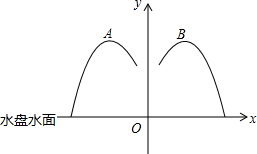 一个台型喷泉,若沿着中轴线截面,得到如图所示的抛物线,一个单位长度是1米,已知这两段抛物线关于y轴对称,其右侧的抛物线为:
一个台型喷泉,若沿着中轴线截面,得到如图所示的抛物线,一个单位长度是1米,已知这两段抛物线关于y轴对称,其右侧的抛物线为: 如图是一个物体的三视图,请画出实物原形的示意图.
如图是一个物体的三视图,请画出实物原形的示意图.