题目内容
若直线y=
x+m和直线y=-
x+m都经过A(-2,0).且与y轴分别交于点B和C,则△ABC中AC边上的高BD= .
| 3 |
| 2 |
| 1 |
| 2 |
考点:两条直线相交或平行问题
专题:计算题
分析:先把A点坐标分别代入y=
x+m和y=-
x+n可求出m、n的值,再根据y轴上点的坐标特征求B点和C点坐标,接着根据三角形面积公式计算△ABC的面积,根据勾股定理计算AC的长,然后利用面积法求BD.
| 3 |
| 2 |
| 1 |
| 2 |
解答:解: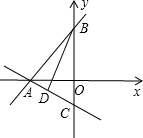 把A(-2,0)代入y=
把A(-2,0)代入y=
x+m得
×(-2)+m=0,解得m=3;把A(-2,0)代入y=-
x+n得-
×(-2)+n=0,解得n=-1,
所以两个一次函数解析式为y=
x+3和y=-
x-1,
当x=0时,y=
x+3=3,则B点坐标为(0,3);当x=0时,y=-
x-1=-1,则C点坐标为(0,-1),
所以△ABC的面积=
×(3+1)×2=4,
因为AC=
=
,
所以
AC•BD=4,
所以BD=
=
.
故答案为
.
 把A(-2,0)代入y=
把A(-2,0)代入y=| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
所以两个一次函数解析式为y=
| 3 |
| 2 |
| 1 |
| 2 |
当x=0时,y=
| 3 |
| 2 |
| 1 |
| 2 |
所以△ABC的面积=
| 1 |
| 2 |
因为AC=
| 12+22 |
| 5 |
所以
| 1 |
| 2 |
所以BD=
| 8 | ||
|
8
| ||
| 5 |
故答案为
8
| ||
| 5 |
点评:本题考查了两直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么他们的自变量系数相同,即k值相同.

练习册系列答案
相关题目
 如图,有一座圆形拱桥,其跨度AB=8m,拱高CD=2m,则弧AB所在圆的半径为( )?
如图,有一座圆形拱桥,其跨度AB=8m,拱高CD=2m,则弧AB所在圆的半径为( )?| A、5m | B、4m | C、3m | D、2m |
如果a<b,那么下列各式中正确的是( )
| A、a-2>b-2 |
| B、a-b<0 |
| C、-2a<-2b |
| D、2a>2b |
在平面直角坐标系中,P(-1,3)关于原点的对称点Q的坐标是( )
| A、(1,3) |
| B、(-1,3) |
| C、(1,-3) |
| D、(-1,-3) |
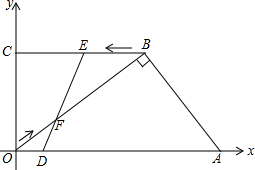 如图,在平面直角坐标系中,A(
如图,在平面直角坐标系中,A(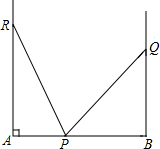 如图,设在一个宽度AB=a的小巷内,一个梯子的长度为b,梯子的脚位于P点,将该梯子的顶端放于一堵墙上Q点时,Q点离地面的高度为c,梯子与地面的夹角为45°,将梯子顶端放于对面一堵墙上R点,离开地面的高度为d,此时梯子与地面的夹角为75°,则d=a,为什么?
如图,设在一个宽度AB=a的小巷内,一个梯子的长度为b,梯子的脚位于P点,将该梯子的顶端放于一堵墙上Q点时,Q点离地面的高度为c,梯子与地面的夹角为45°,将梯子顶端放于对面一堵墙上R点,离开地面的高度为d,此时梯子与地面的夹角为75°,则d=a,为什么?