题目内容
18.阅读下列材料:计算:$\frac{1}{24}$÷﹙$\frac{1}{3}$-$\frac{1}{4}$+$\frac{1}{12}$﹚.
解法一:原式=$\frac{1}{24}$÷$\frac{1}{3}$-$\frac{1}{24}$÷$\frac{1}{4}$+$\frac{1}{24}$÷$\frac{1}{12}$=$\frac{1}{24}$×3-$\frac{1}{24}$×4+$\frac{1}{24}$×12=$\frac{11}{24}$.
解法二:原式=$\frac{1}{24}$÷﹙$\frac{4}{12}$-$\frac{3}{12}$+$\frac{1}{12}$﹚=$\frac{1}{24}$÷$\frac{2}{12}$=$\frac{1}{24}$×6=$\frac{1}{4}$.
解法三:原式的倒数=﹙$\frac{1}{3}$-$\frac{1}{4}$+$\frac{1}{12}$﹚÷$\frac{1}{24}$=﹙$\frac{1}{3}$-$\frac{1}{4}$+$\frac{1}{12}$﹚×24=$\frac{1}{3}$×24-$\frac{1}{4}$×24+$\frac{1}{12}$×24=4.
所以,原式=$\frac{1}{4}$.
(1)上述得到的结果不同,你认为解法一是错误的;
(2)请你选择合适的解法计算:﹙-$\frac{1}{42}$﹚÷﹙$\frac{1}{6}$-$\frac{3}{14}$+$\frac{2}{3}$-$\frac{2}{7}$﹚.
分析 (1)我认为解法一是错误的;
(2)选择解法三求出值即可.
解答 解:(1)上述得到的结果不同,我认为解法一是错误的;
故答案为:一;
(2)原式的倒数为原式的倒数为:($\frac{1}{6}$-$\frac{3}{14}$+$\frac{2}{3}$-$\frac{2}{7}$)÷(-$\frac{1}{42}$)=($\frac{1}{6}$-$\frac{3}{14}$+$\frac{2}{3}$-$\frac{2}{7}$)×(-42)=-7+9-28+12=-35+21=-14,
则原式=-$\frac{1}{14}$.
点评 此题考查了有理数的除法,熟练掌握除法法则是解本题的关键.

练习册系列答案
相关题目
9.-$|{-\frac{1}{2}}|$的倒数是( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
10.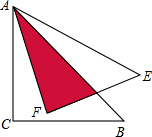 如图,将等腰直角三角形ABC绕点A逆时针旋转15度得到△AEF,若AC=$\sqrt{3}$,则阴影部分的面积为( )
如图,将等腰直角三角形ABC绕点A逆时针旋转15度得到△AEF,若AC=$\sqrt{3}$,则阴影部分的面积为( )
 如图,将等腰直角三角形ABC绕点A逆时针旋转15度得到△AEF,若AC=$\sqrt{3}$,则阴影部分的面积为( )
如图,将等腰直角三角形ABC绕点A逆时针旋转15度得到△AEF,若AC=$\sqrt{3}$,则阴影部分的面积为( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\sqrt{3}$ |
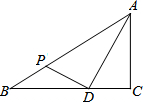 如图,△ABC中,∠C=90°,AD平分∠BAC,BD=4cm,CD=3cm,点P是边AB上的动点,则DP长的最小值为3cm.
如图,△ABC中,∠C=90°,AD平分∠BAC,BD=4cm,CD=3cm,点P是边AB上的动点,则DP长的最小值为3cm.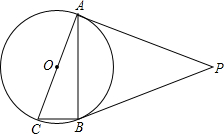 如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是圆外一点,PA切⊙O于点A,且PA=PB.
如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是圆外一点,PA切⊙O于点A,且PA=PB.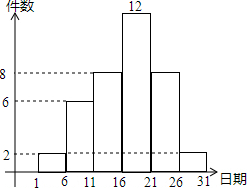 在学校开展的综合实践活动中,八年级某班对本班的40名学生进行了小制作评比,作品上交时间为5月1日至31日,评委把同学们上交作品的件数按5天一组分组统计,绘制了频数直方图(如图),图中从左到右依次为第一、二、三、四、五、六组.
在学校开展的综合实践活动中,八年级某班对本班的40名学生进行了小制作评比,作品上交时间为5月1日至31日,评委把同学们上交作品的件数按5天一组分组统计,绘制了频数直方图(如图),图中从左到右依次为第一、二、三、四、五、六组.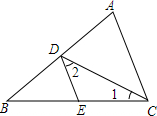 如图所示,CD是△ABC的角平分线,E是BC边上的一点,且∠1=∠2.试判断DE与AC的位置关系并说明理由.
如图所示,CD是△ABC的角平分线,E是BC边上的一点,且∠1=∠2.试判断DE与AC的位置关系并说明理由.