题目内容
6.设(2x-1)6=a0+a1x+a2x2+…+a6x6,则a1+a2+a3+a4+a5=1.分析 由题意(2x-1)6=a0x6+a1x5+a2x4+a3x3+a4x2+a5x+a6,可以令x=1,即可求解.
解答 解:∵(2x-1)6=a0x6+a1x5+a2x4+a3x3+a4x2+a5x+a6,
令x=1得,(2-1)6=a0+a1+a2+a3+a4+a5+a6,
∴a0+a1+a2+a3+a4+a5+a6=1,
故答案为:1.
点评 此题主要考查代数式求解,解题的关键是取特值法,即令x=1,然后求解.此题是一道经典类型的题,大家要掌握好.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
14.若分式$\frac{x}{x-1}$有意义,则x的取值范围是( )
| A. | x>1 | B. | x=1 | C. | x<1 | D. | x≠1 |
1.要使分式$\frac{x-1}{x+1}$有意义,则x应满足的条件是( )
| A. | x≠-1 | B. | x≠1 | C. | x<-1 | D. | x>-1 |
18. 如图,已知A、B两村分别距公路l的距离AA′=10km,BB′=40km,且A′B′=50km.在公路l上建一中转站P使AP+BP的值最小,则AP+BP的最小值为( )
如图,已知A、B两村分别距公路l的距离AA′=10km,BB′=40km,且A′B′=50km.在公路l上建一中转站P使AP+BP的值最小,则AP+BP的最小值为( )
 如图,已知A、B两村分别距公路l的距离AA′=10km,BB′=40km,且A′B′=50km.在公路l上建一中转站P使AP+BP的值最小,则AP+BP的最小值为( )
如图,已知A、B两村分别距公路l的距离AA′=10km,BB′=40km,且A′B′=50km.在公路l上建一中转站P使AP+BP的值最小,则AP+BP的最小值为( )| A. | 100km | B. | 80km | C. | 60km | D. | 50$\sqrt{2}$km |
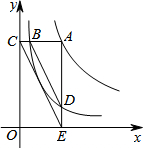 如图,已知反比例函数y1=$\frac{1}{x}$、y2=$\frac{4}{x}$在第一象限的图象,过y2上的任意一点A,作x轴的平行线交y1于B,交y轴于点C,过点A作x轴的垂线交y1于D,交x轴于点E,连接BD、CD,则$\frac{BD}{CE}$=$\frac{3}{4}$.
如图,已知反比例函数y1=$\frac{1}{x}$、y2=$\frac{4}{x}$在第一象限的图象,过y2上的任意一点A,作x轴的平行线交y1于B,交y轴于点C,过点A作x轴的垂线交y1于D,交x轴于点E,连接BD、CD,则$\frac{BD}{CE}$=$\frac{3}{4}$.