题目内容
梯形ABCD中,AB∥CD,AB=kAC,E为腰BC上一点,且∠AED=∠BAC.
(1)如图1,当k=1时,试判断AE与DE的数量关系,并加以证明.
(2)如图2,当k≠1时,∠ACB<90°,其它条件不变,(1)中结论还成立吗?如果成立,请加以证明;如果不成立,写出新的数量关系,并加以证明.

(1)如图1,当k=1时,试判断AE与DE的数量关系,并加以证明.
(2)如图2,当k≠1时,∠ACB<90°,其它条件不变,(1)中结论还成立吗?如果成立,请加以证明;如果不成立,写出新的数量关系,并加以证明.

考点:四边形综合题
专题:
分析:(1)求出A、D、C、E四点共圆,推出∠ADE=∠ACB,求出∠ADE=∠DAE,根据等腰三角形的判定推出即可;
(2)求出A、D、C、E四点共圆,推出∠ADE=∠ACB,推出△ADE和△ACB相似,得出比例式,求出即可.
(2)求出A、D、C、E四点共圆,推出∠ADE=∠ACB,推出△ADE和△ACB相似,得出比例式,求出即可.
解答:(1)AE=DE,
证明:∵AB∥CD,
∴∠DCA=∠BAC,
∵∠AED=∠BAC,
∴∠DCA=∠DEA,
∴A、D、C、E四点共圆,
∴∠ADE=∠ACB,
∵AB=kAC,k=1,
∴∠B=∠ACB,
∴∠DAE=∠ADE,
∴AE=DE;
(2)(1)中的结论不成立,
AE=kDE,
证明:∵AB∥CD,
∴∠DCA=∠BAC,
∵∠AED=∠BAC,
∴∠DCA=∠DEA,
∴A、D、C、E四点共圆,
∴∠ADE=∠ACB,
∵∠BAC=∠DEA,
∴△ADE∽△BCA,
∴
=
,
∴∠B=∠ACB,
∴∠DAE=∠ADE,AB=kAC,
∴AE=kDE.
证明:∵AB∥CD,
∴∠DCA=∠BAC,
∵∠AED=∠BAC,
∴∠DCA=∠DEA,
∴A、D、C、E四点共圆,
∴∠ADE=∠ACB,
∵AB=kAC,k=1,
∴∠B=∠ACB,
∴∠DAE=∠ADE,
∴AE=DE;
(2)(1)中的结论不成立,
AE=kDE,
证明:∵AB∥CD,
∴∠DCA=∠BAC,
∵∠AED=∠BAC,
∴∠DCA=∠DEA,
∴A、D、C、E四点共圆,
∴∠ADE=∠ACB,
∵∠BAC=∠DEA,
∴△ADE∽△BCA,
∴
| DE |
| AE |
| AC |
| AB |
∴∠B=∠ACB,
∴∠DAE=∠ADE,AB=kAC,
∴AE=kDE.
点评:本题考查了四点共圆的条件,圆周角定理,相似三角形的性质和判定,全等三角形的性质和判定的应用,主要考查了学生的推理能力,题目比较好,有一定难度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知:如图,等腰△ABC的周长是32cm,底边长是12cm,
已知:如图,等腰△ABC的周长是32cm,底边长是12cm, 如图,有长为24米的篱笆,一面用墙(墙的最大可用长度a=15米)围成中间隔有一道篱笆的长方形花圃,设围成的花圃的面积为y平方米,AB长为x米.
如图,有长为24米的篱笆,一面用墙(墙的最大可用长度a=15米)围成中间隔有一道篱笆的长方形花圃,设围成的花圃的面积为y平方米,AB长为x米.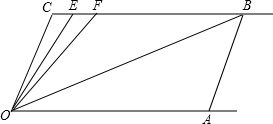 如图,直线CB∥OA,∠C=∠OAB=100°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF
如图,直线CB∥OA,∠C=∠OAB=100°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF 如图,△ABC中,∠B=30°,∠C=45°,AD⊥BC于D,若AB=8,则CD=
如图,△ABC中,∠B=30°,∠C=45°,AD⊥BC于D,若AB=8,则CD=