题目内容
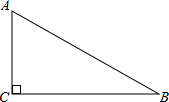 如图,在△ABC中,∠C=90°,∠B=30°.
如图,在△ABC中,∠C=90°,∠B=30°.(1)用尺规法作出∠A的平分线;
(2)若AD是△ABC的角平分线,且AD=2
| 3 |
考点:作图—基本作图
专题:
分析:(1)利用角平分线的作法得出即可;
(2)利用直角三角形中30°所对的边等于斜边的一半以及结合勾股定理进而求出即可.
(2)利用直角三角形中30°所对的边等于斜边的一半以及结合勾股定理进而求出即可.
解答: 解:(1)如图所示:AD即为所求;
解:(1)如图所示:AD即为所求;
(2)∵在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,
∴∠CAD=∠DAB=∠B=30°,
∴CD=
AD=
,
∴AC=3,
∴AB=2AC=6.
 解:(1)如图所示:AD即为所求;
解:(1)如图所示:AD即为所求;(2)∵在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,
∴∠CAD=∠DAB=∠B=30°,
∴CD=
| 1 |
| 2 |
| 3 |
∴AC=3,
∴AB=2AC=6.
点评:此题主要考查了基本作图以及勾股定理以及直角三角形的性质,得出AC与AB的关系是解题关键.

练习册系列答案
相关题目
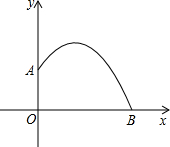 北京时间5月18日-25日,2014年世界羽联汤姆斯杯尤伯杯决赛在印度首都新德里进行,在比赛中,某次羽毛球的运动路线可以看作是抛物线y=-
北京时间5月18日-25日,2014年世界羽联汤姆斯杯尤伯杯决赛在印度首都新德里进行,在比赛中,某次羽毛球的运动路线可以看作是抛物线y=-| 1 |
| 4 |
| 3 |
| 4 |
| A、出球点A离地面点O的距离是1m | ||
| B、该羽毛球横向飞出的最远距离是3m | ||
C、此次羽毛球最高可达到
| ||
D、当羽毛球横向飞出
|
 如图,∠AOB=2∠BOC,求证:∠ACB=2∠BAC.
如图,∠AOB=2∠BOC,求证:∠ACB=2∠BAC. △ABC中,BC=48cm,高AD=16cm,它的内接矩形EFMN的两边EF:FM=5:9,求矩形的周长.
△ABC中,BC=48cm,高AD=16cm,它的内接矩形EFMN的两边EF:FM=5:9,求矩形的周长.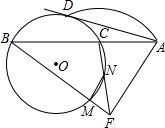 已知:如图,AD切⊙O于点D,ACB为⊙O的割线,AP=AD,BP、CP分别交⊙O于M、N.求证:
已知:如图,AD切⊙O于点D,ACB为⊙O的割线,AP=AD,BP、CP分别交⊙O于M、N.求证: