题目内容
 如图,点A是双曲线y=
如图,点A是双曲线y=| 1 |
| x |
①逐渐变小;
②由大变小再由小变大;
③由小变大再由大变小;
④不变.
你认为正确的是
考点:反比例函数系数k的几何意义
专题:
分析:四边形ABCD的面积等于
×AC×BD,AC、BC可以用A点的坐标表示,即可求解.
| 1 |
| 2 |
解答:解:设A点的坐标是(m,n),则m•n=1,则D点的横坐标是
m,
把x=
m代入y=
,得到y=
,即BD=
.
∴四边形ABCD的面积=
AC×BD=
×m×
=1.
即四边形ABCD的面积不随A点的变化而变化.
故答案为④.
| 1 |
| 2 |
把x=
| 1 |
| 2 |
| 1 |
| x |
| 2 |
| m |
| 2 |
| m |
∴四边形ABCD的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| m |
即四边形ABCD的面积不随A点的变化而变化.
故答案为④.
点评:本题主要考查的是利用反比例函数系数k的几何意义求对角线互相垂直的四边形面积的计算方法.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
将正六边形绕其对称中心点O旋转一个小于180°的角后与原图形重合,这个旋转的角度是( )
| A、120° | B、90° |
| C、60° | D、60°或120° |
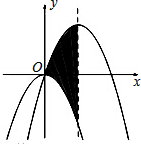 如图,在平面直角坐标系中,抛物线y1=-
如图,在平面直角坐标系中,抛物线y1=-| 1 |
| 2 |
| 1 |
| 2 |
| A、12 | B、12.5 |
| C、13 | D、13.5 |
 如图,把一张长方形纸条ABCD沿AF折叠,点B对应点E,已知∠ADB=30°,当∠BAF的度数为
如图,把一张长方形纸条ABCD沿AF折叠,点B对应点E,已知∠ADB=30°,当∠BAF的度数为 如图是七年级(1)班参加课外兴趣小组人数的扇形统计图,则表示唱歌兴趣小组人数的扇形的圆心角度数是
如图是七年级(1)班参加课外兴趣小组人数的扇形统计图,则表示唱歌兴趣小组人数的扇形的圆心角度数是 △ABC是等边三角形,把∠A按如图折叠,则∠1+∠2=
△ABC是等边三角形,把∠A按如图折叠,则∠1+∠2=