题目内容
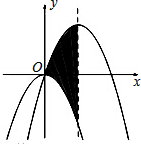 如图,在平面直角坐标系中,抛物线y1=-
如图,在平面直角坐标系中,抛物线y1=-| 1 |
| 2 |
| 1 |
| 2 |
| A、12 | B、12.5 |
| C、13 | D、13.5 |
考点:二次函数图象与几何变换
专题:计算题
分析:先把y2=-
x2+3x配成顶点式得到抛物线y2=-
(x-3)2+
,则它的顶点坐标为(3,
),所以抛物线y1=-
x2先向右平移3个单位,再向上平移
个单位得到抛物线y2=-
x2+3x,然后把阴影部分的面积转化为矩形的面积后求解.
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
| 9 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
| 1 |
| 2 |
解答:解:抛物线y1=-
x2的顶点坐标为(0,0),抛物线y2=-
x2+3x=-
(x-3)2+
的顶点坐标为(3,
),
所以抛物线y1=-
x2先向右平移3个单位,再向上平移
个单位得到抛物线y2=-
x2+3x,
所以对称轴与两段抛物线所围成的阴影部分的面积=3×
=13.5.
故选D.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
| 9 |
| 2 |
所以抛物线y1=-
| 1 |
| 2 |
| 9 |
| 2 |
| 1 |
| 2 |
所以对称轴与两段抛物线所围成的阴影部分的面积=3×
| 9 |
| 2 |
故选D.
点评:本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.

练习册系列答案
相关题目
若
+|
+2|=0,则yx的值等于( )
| x-2 |
| 3 | y |
| A、-36 | B、-64 |
| C、36 | D、64 |
已知1≤a≤
,化简
+|a-2|的结果是( )
| 2 |
| a2-2a+1 |
| A、2a-3 | B、2a+3 |
| C、3 | D、1 |
如果方程组
的解
,则方程组
的解为( )
|
|
|
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
下列各等式中成立的是( )
A、-
| ||
B、-
| ||
C、
| ||
D、
|
若a>b,则下列不等式的变形错误的是( )
| A、-8+a>-8+b | ||||
| B、-3a>-3b | ||||
| C、a+5>b+5 | ||||
D、
|
 如图,点A是双曲线y=
如图,点A是双曲线y=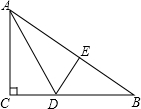 如图,有一个直角三角形纸片,两直角边AC=18cm,BC=24cm,现将直角边AC沿直线AD折叠,若点C恰好落在斜边AB上的点E处,求BD的长.
如图,有一个直角三角形纸片,两直角边AC=18cm,BC=24cm,现将直角边AC沿直线AD折叠,若点C恰好落在斜边AB上的点E处,求BD的长.