题目内容
10.已知:31=3,32=9,33=27,34=81,35=243,36=729…,设A=2(3+1)(32+1)(34+1)(316+1)(332+1)+1,则A的个位数字是1.分析 A中2变形后,利用平方差公式化简,归纳总结得到一般性规律,即可确定出A的个位数字.
解答 解:A=(3-1)(3+1)(32+1)(34+1)(316+1)(332+1)+1
=(32-1)(32+1)(34+1)(316+1)(332+1)+1
=(34-1)(34+1)(316+1)(332+1)+1
=(316-1)(316+1)(332+1)+1
=(332-1)(332+1)+1
=364-1+1
=364,
观察已知等式,个位数字以3,9,7,1循环,
则A的个位数字是1,
故答案为:1.
点评 此题考查了平方差公式,熟练掌握平方差公式是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18. 某个不等式组的解集在数轴上表示如图,则这个不等式组可能是( )
某个不等式组的解集在数轴上表示如图,则这个不等式组可能是( )
 某个不等式组的解集在数轴上表示如图,则这个不等式组可能是( )
某个不等式组的解集在数轴上表示如图,则这个不等式组可能是( )| A. | $\left\{\begin{array}{l}{x>5}\\{x≥1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x<5}\\{x≥-1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x>5}\\{x>-1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x<5}\\{x>-1}\end{array}\right.$ |
5.若(x+m)2=x2+kx+4是一个完全平方式,则k的值是( )
| A. | 2 | B. | 4 | C. | ±2 | D. | ±4 |
15.不等式4+2x>0的解集是( )
| A. | 2x>4 | B. | x>2 | C. | x>-2 | D. | x<-2 |
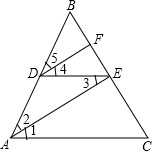
 如图,在平面直角坐标系中,已知A,B,C三点的坐标分别为(0,a)(b,0)(b,c)(如图所示),其中a,b,c满足关系式(a-2)2+$\sqrt{b-3}$=0,|c-4|≤0.
如图,在平面直角坐标系中,已知A,B,C三点的坐标分别为(0,a)(b,0)(b,c)(如图所示),其中a,b,c满足关系式(a-2)2+$\sqrt{b-3}$=0,|c-4|≤0.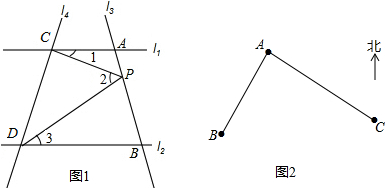
 阅读下列推理过程,在括号中填写理由.
阅读下列推理过程,在括号中填写理由.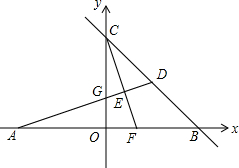 如图,在平面直角坐标系中,A,B,C为坐标轴上的三点,且OA=OB=OC=4,过点A的直线AD交BC于点D,交y轴于点G,△ABD的面积为8.过点C作CE⊥AD,交AB交于F,垂足为E.
如图,在平面直角坐标系中,A,B,C为坐标轴上的三点,且OA=OB=OC=4,过点A的直线AD交BC于点D,交y轴于点G,△ABD的面积为8.过点C作CE⊥AD,交AB交于F,垂足为E.