题目内容
10.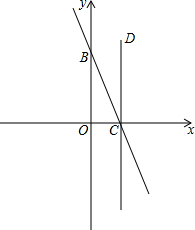 如图,直线y=-2x+4与坐标轴分别交于C、B两点,过点C作CD⊥x轴,点P是x轴下方直线CD上的一点,且△OCP与△OBC相似,求过点P的双曲线解析式.
如图,直线y=-2x+4与坐标轴分别交于C、B两点,过点C作CD⊥x轴,点P是x轴下方直线CD上的一点,且△OCP与△OBC相似,求过点P的双曲线解析式.
分析 由直线y=-2x+4与坐标轴分别交于C、B两点,易得OC=2,OB=4,再分两种情况①当∠OBC=∠COP时,△OCP与△OBC相似,②当∠OBC=∠CPO时,△OCP与△OBC相似分别求出点的坐标,再求出过点P的双曲线解析式.
解答 解:∵直线y=-2x+4与坐标轴分别交于C、B两点,
∴令y=0,可得-2x+4=0,解得x=2,即C(2,0),OC=2,
令x=0,可得y=4,即B(0,4),OB=4,
①如图1,当∠OBC=∠COP时,△OCP∽△BOC,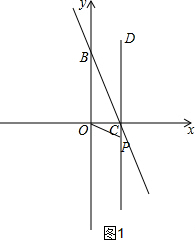
∴$\frac{OB}{OC}$=$\frac{OC}{CP}$,即$\frac{4}{2}$=$\frac{2}{CP}$,解得CP=1,
∴P(2,-1),
设过点P的双曲线解析式y=$\frac{k}{x}$,把P点代入解得k=-2,
∴过点P的双曲线解析式y=-$\frac{2}{x}$,
②如图2,当∠OBC=∠CPO时,△OCP∽△COB,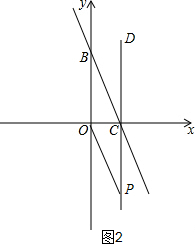
在△OCP和△COB中,
$\left\{\begin{array}{l}{∠OBC=∠CPO}\\{∠COB=∠OCP}\\{OC=CO}\end{array}\right.$
∴△OCP≌△COB(AAS)
∴CP=BO=4,
∴P(2,-4)
设过点P的双曲线解析式y=$\frac{k}{x}$,把P点代入得-4=$\frac{k}{2}$,解得k=-8,
∴过点P的双曲线解析式y=$\frac{-8}{x}$.
综上可得,过点P的双曲线的解析式为y=-$\frac{2}{x}$或y=$\frac{-8}{x}$.
点评 本题主要考查了相似三角形的判定与性质,待定系数求反比例函数,解题的关键是分两种情况正确画出图形.

练习册系列答案
相关题目
1.$\sqrt{({-2015)}^{2}}$=( )
| A. | -2015 | B. | 2015 | C. | ±2015 | D. | $\frac{1}{2015}$ |
15.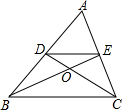 如图,在△ABC中,两条中线BE,CD相交于点O,则S△DOE:S△DCE=( )
如图,在△ABC中,两条中线BE,CD相交于点O,则S△DOE:S△DCE=( )
 如图,在△ABC中,两条中线BE,CD相交于点O,则S△DOE:S△DCE=( )
如图,在△ABC中,两条中线BE,CD相交于点O,则S△DOE:S△DCE=( )| A. | 1:4 | B. | 1:3 | C. | 1:2 | D. | 2:3 |
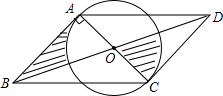 如图,平行四边形ABCD中,AB=AC=4,AB⊥AC,O是对角线的交点,若⊙O过A、C两点,则图中阴影部分的面积之和为4.
如图,平行四边形ABCD中,AB=AC=4,AB⊥AC,O是对角线的交点,若⊙O过A、C两点,则图中阴影部分的面积之和为4.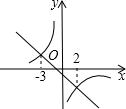 定义运算max{a,b}:当a≥b时,max{a,b}=a;当a<b时,max{a,b}=b.如max{-3,2}=2.
定义运算max{a,b}:当a≥b时,max{a,b}=a;当a<b时,max{a,b}=b.如max{-3,2}=2.