题目内容
16.如图1,P是反比例函数y=$\frac{6}{x}$(x>0)上的一个动点,过P作PA⊥x轴,PB⊥y轴.(1)若矩形OAPB的长是宽的两倍,求P点坐标;
(2)若矩形对角线AB=6,求矩形OAPB的周长;
(3)如图2,E在BP上,且BE=2PE,若E关于直线AB的对称点F恰好落在坐标轴上,连结AE,AF,EF,求△AEF的面积.
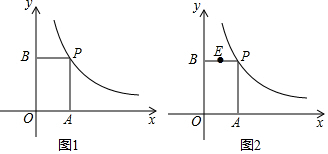
分析 (1)利用反比例函数k的几何意义得到矩形OAPB的面积=6,设矩形OAPB的宽为m,则长为2m,利用矩形的面积公式可计算出m=$\sqrt{3}$,从而得到P点坐标;
(2)设矩形OAPB的两边为m、n,利用反比例函数k的几何意义得到mn=6,再根据勾股定理得到a2+b2=62,根据完全平分公式变形得到(a+b)2-2ab=36,则可计算出a+b=4$\sqrt{3}$,
从而得到矩形OAPB的周长;
(3)当E关于直线AB的对称点F恰好落在x轴上,如图2,AB与EF相交于点Q,利用三角形面积公式得到S△ABE=2,再根据对称轴的性质得AB垂直平分EF,EQ=FQ,接着证明FQ垂直平分AB得到BQ=AQ,所以S△AQE=$\frac{1}{2}$S△ABE=1,则S△AEF=2S△AQE=2;当E关于直线AB的对称点F恰好落在y轴上,如图3,证明四边形OAPB为正方形得到P($\sqrt{6}$,$\sqrt{6}$),则可计算出S△BEF=$\frac{4}{3}$,而S△AOE=S△APE=1,于是得到S△AEF=$\frac{8}{3}$.
解答 解:(1)∵PA⊥x轴,PB⊥y轴,
∴矩形OAPB的面积=|k|=6,
设矩形OAPB的宽为m,则长为2m,
∴m•2m=6,解得m=$\sqrt{3}$,
∴P点坐标为($\sqrt{3}$,2$\sqrt{3}$)或(2$\sqrt{3}$,$\sqrt{3}$);
(2)设矩形OAPB的两边为m、n,则mn=6,
∵矩形对角线AB=6,
∴a2+b2=62,
∴(a+b)2-2ab=36,
∴(a+b)2=36+2×6,
∴a+b=4$\sqrt{3}$,
∴矩形OAPB的周长为8$\sqrt{3}$;
(3)当E关于直线AB的对称点F恰好落在x轴上,如图2,AB与EF相交于点Q,
∵矩形OAPB的面积=6,
而BE=2PE,
∴S△ABE=2,
∵点E与点F关于AB对称,
∴AB垂直平分EF,EQ=FQ,
∴AE=AF,
∴∠AEF=∠AFE,
∵PB∥OA,
∴∠AFE=∠BEF,
∴∠BEF=∠AEF,
∴FQ垂直平分AB,
∴BQ=AQ,
∴S△AQE=$\frac{1}{2}$S△ABE=1,
∴S△AEF=2S△AQE=2;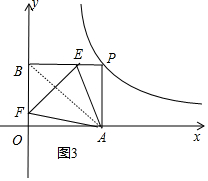
当E关于直线AB的对称点F恰好落在y轴上,如图3,
∵点E与点F关于AB对称,
∴BE=BF,AB⊥EF,
∴△BEF为等腰直角三角形,
∴AB平分∠OBP,
∴四边形OAPB为正方形,
∴P($\sqrt{6}$,$\sqrt{6}$),
∴BE=BF=$\frac{2\sqrt{6}}{3}$,
∴S△BEF=$\frac{1}{2}$•$\frac{2\sqrt{6}}{3}$•$\frac{2\sqrt{6}}{3}$=$\frac{4}{3}$,
而S△AOE=S△APE=1,
∴S△AEF=6-$\frac{4}{3}$-1-1=$\frac{8}{3}$,
综上所述,△AEF的面积为2或$\frac{8}{3}$.
点评 本题考查了反比例函数的综合题:熟练掌握反比例函数图象上点的坐标特征、反比例函数k的几何意义和轴对称的性质;灵活运用矩形的性质进行几何计算;理解坐标与图形性质.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 已知点O(0,0),B(1,2).
已知点O(0,0),B(1,2).
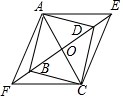 如图,在?ABCD中,对角线AC、BD相交于点O,OA=5cm,E、F为直线BD上的两个动点(点E、F始终在?ABCD的外面),且DE=$\frac{1}{2}$OD,BF=$\frac{1}{2}$OB,连接AE、CE、CF、AF.
如图,在?ABCD中,对角线AC、BD相交于点O,OA=5cm,E、F为直线BD上的两个动点(点E、F始终在?ABCD的外面),且DE=$\frac{1}{2}$OD,BF=$\frac{1}{2}$OB,连接AE、CE、CF、AF.