题目内容
5. 如图,菱形ABCD中,0是AC中点,EF经过点O,分别交AD,CB的延长线于点E,F.
如图,菱形ABCD中,0是AC中点,EF经过点O,分别交AD,CB的延长线于点E,F.(1)求证:四边形AFCE是平行四边形;
(2)已知AB=a,∠DAB=α(0<α<90°).
①试问四边形AFCE是否可能为矩形?若可能,请用α表示∠AOE的度数;若没可能,请说明理由;
②直接写出当S四边形ABCD=$\frac{\sqrt{3}}{2}$S四边形AFCE时DE的长(用含α的代数式表示).
分析 (1)由△AOE≌△COF,得到OE=OF,OA=OC,由此即可证明.
(2)根据矩形的性质得到OA=OE,由∠AOE=180°-(∠OAE+∠OEA)即可解决问题.
(3)把条件S四边形ABCD=$\frac{\sqrt{3}}{2}$S四边形AFCE,转化为AD=$\frac{\sqrt{3}}{2}$AE,即可解决问题.
解答 (1)证明:如图1中,∵四边形ABCD是菱形,
∴AD∥BC,
∴∠EAO=∠FCO,
在△AOE和△COF中,
$\left\{\begin{array}{l}{∠EAO=∠FCO}\\{AO=OC}\\{∠AOE=∠FOC}\end{array}\right.$,
∴△AOE≌△COF,
∴OE=OF,∵OA=OC,
∴四边形AFCE是平行四边形.
(2)①四边形AFCE能为矩形.
理由:如图1中,当OA=OC=OE=OF时,四边形AFCE是矩形.
此时∠OAE=∠OEA=$\frac{1}{2}$α,
∴∠AOE=180°-(∠OAE+∠OEA)=180°-α.
②如图2中,连接BD.
∵四边形ABCD是菱形,
∴AC与BD交于点O,
∵四边形AFCE是平行四边形,
∴S△AOF=$\frac{1}{4}$S四边形ABCD,S△AOD=$\frac{1}{4}$S四边形AFCE,
∵S四边形ABCD=$\frac{\sqrt{3}}{2}$S四边形AFCE,
∴AD=$\frac{\sqrt{3}}{2}$AE,
∵AD=AB=a,
∴a=$\frac{\sqrt{3}}{2}$(a+DE),
∴DE=$\frac{2\sqrt{3}-3}{3}$a.
点评 本题考查四边形综合题、全等三角形的判定和性质、菱形的性质、平行四边形的性质等知识,解题的关键是熟练应用这些知识解决问题,属于中考常考题型.

 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 如图,⊙O的直径AB=12,弦CD⊥AB,∠C=30°,则S阴影等于( )
如图,⊙O的直径AB=12,弦CD⊥AB,∠C=30°,则S阴影等于( )| A. | 6π | B. | 2π | C. | $\frac{π}{6}$ | D. | $\frac{π}{2}$ |
| A. | $\left\{\begin{array}{l}{x+y=100}\\{(1+10%)x+(1-40%)y=100×(1+20%)}\end{array}\right.$ | |
| B. | $\left\{\begin{array}{l}{x+y=100}\\{(1-10%)x+(1+40%)y=100×(1+20%)}\end{array}\right.$ | |
| C. | $\left\{\begin{array}{l}{x+y=100}\\{(1-10%)x+(1+40%)y=100×20%}\end{array}\right.$ | |
| D. | $\left\{\begin{array}{l}{x+y=100}\\{(1+10%)x+(1-40%)y=100×20%}\end{array}\right.$ |
 已知数据总数是30,在样本频数分布直方图(如图)中,各小长方形的高之比为AE:BF:CG:DH=2:4:3:1,第二小组的频数为12.
已知数据总数是30,在样本频数分布直方图(如图)中,各小长方形的高之比为AE:BF:CG:DH=2:4:3:1,第二小组的频数为12.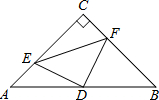 如图,△ABC是等腰三角形,∠C=90°,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE,DF,EF.在此运动变化过程中,有下列结论:
如图,△ABC是等腰三角形,∠C=90°,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE,DF,EF.在此运动变化过程中,有下列结论: 如图,四边形ABCD的对角线AC,BD交于点O,已知O是AC的中点,AE=CF,DF∥BE.
如图,四边形ABCD的对角线AC,BD交于点O,已知O是AC的中点,AE=CF,DF∥BE. 如图,在△ABC中,AB=AC,AD是BC边上的中线,以AD为直径作⊙O,连接BO并延长至点E,使得OE=OB,交⊙O于点F,连接AE,CE.
如图,在△ABC中,AB=AC,AD是BC边上的中线,以AD为直径作⊙O,连接BO并延长至点E,使得OE=OB,交⊙O于点F,连接AE,CE.