题目内容
4.因式分解法:(x-4)2=(5-2x)2.分析 移项得(x-4)2-(5-2x)2=0,然后利用平方差公式得到(-x+1)(3x-9)=0,从而得到答案.
解答 解:∵(x-4)2=(5-2x)2,
∴(x-4)2-(5-2x)2=0,
∴(x-4+5-2x)(x-4-5+2x)=0,
∴(-x+1)(3x-9)=0,
∴x1=1,x2=3.
点评 本题主要考查了因式分解法解一元二次方程的知识,解方程的一般步骤:①移项,使方程的右边化为零;②将方程的左边分解为两个一次因式的乘积;③令每个因式分别为零,得到两个一元一次方程;④解这两个一元一次方程,它们的解就都是原方程的解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.若|x-2|=2-x,则x的取值范围是( )
| A. | x<2 | B. | x≤2 | C. | x>2 | D. | x≥2 |
14.一个多边形的每一个外角都等于40°,则这个多边形的边数为( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
 折叠矩形纸片ABCD,使点D落在BC边的点F处,已知AB=8,BC=10,则EC=3.
折叠矩形纸片ABCD,使点D落在BC边的点F处,已知AB=8,BC=10,则EC=3.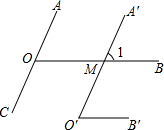 如图所示,OA∥O′A′,OB∥O′B′.
如图所示,OA∥O′A′,OB∥O′B′.